Purdue Online Writing Lab Purdue OWL® College of Liberal Arts

Basic Inferential Statistics: Theory and Application

Welcome to the Purdue OWL
This page is brought to you by the OWL at Purdue University. When printing this page, you must include the entire legal notice.
Copyright ©1995-2018 by The Writing Lab & The OWL at Purdue and Purdue University. All rights reserved. This material may not be published, reproduced, broadcast, rewritten, or redistributed without permission. Use of this site constitutes acceptance of our terms and conditions of fair use.
The heart of statistics is inferential statistics. Descriptive statistics are typically straightforward and easy to interpret. Unlike descriptive statistics, inferential statistics are often complex and may have several different interpretations.
The goal of inferential statistics is to discover some property or general pattern about a large group by studying a smaller group of people in the hopes that the results will generalize to the larger group. For example, we may ask residents of New York City their opinion about their mayor. We would probably poll a few thousand individuals in New York City in an attempt to find out how the city as a whole views their mayor. The following section examines how this is done.
A population is the entire group of people you would like to know something about. In our previous example of New York City, the population is all of the people living in New York City. It should not include people from England, visitors in New York, or even people who know a lot about New York City.
A sample is a subset of the population. Just like you may sample different types of ice cream at the grocery store, a sample of a population should be just a smaller version of the population.
It is extremely important to understand how the sample being studied was drawn from the population. The sample should be as representative of the population as possible. There are several valid ways of creating a sample from a population, but inferential statistics works best when the sample is drawn at random from the population. Given a large enough sample, drawing at random ensures a fair and representative sample of a population.
Comparing two or more groups
Much of statistics, especially in medicine and psychology, is used to compare two or more groups and attempts to figure out if the two groups are different from one another.
Example: Drug X
Let us say that a drug company has developed a pill, which they think increases the recovery time from the common cold. How would they actually find out if the pill works or not? What they might do is get two groups of people from the same population (say, people from a small town in Indiana who had just caught a cold) and administer the pill to one group, and give the other group a placebo. They could then measure how many days each group took to recover (typically, one would calculate the mean of each group). Let's say that the mean recovery time for the group with the new drug was 5.4 days, and the mean recovery time for the group with the placebo was 5.8 days.
The question becomes, is this difference due to random chance, or does taking the pill actually help you recover from the cold faster? The means of the two groups alone does not help us determine the answer to this question. We need additional information.
Sample Size
If our example study only consisted of two people (one from the drug group and one from the placebo group) there would be so few participants that we would not have much confidence that there is a difference between the two groups. That is to say, there is a high probability that chance explains our results (any number of explanations might account for this, for example, one person might be younger, and thus have a better immune system). However, if our sample consisted of 1,000 people in each group, then the results become much more robust (while it might be easy to say that one person is younger than another, it is hard to say that 1,000 random people are younger than another 1,000 random people). If the sample is drawn at random from the population, then these 'random' variations in participants should be approximately equal in the two groups, given that the two groups are large. This is why inferential statistics works best when there are lots of people involved.
Be wary of statistics that have small sample sizes, unless they are in a peer-reviewed journal. Professional statisticians can interpret results correctly from small sample sizes, and often do, but not everyone is a professional, and novice statisticians often incorrectly interpret results. Also, if your author has an agenda, they may knowingly misinterpret results. If your author does not give a sample size, then he or she is probably not a professional, and you should be wary of the results. Sample sizes are required information in almost all peer-reviewed journals, and therefore, should be included in anything you write as well.
Variability
Even if we have a large enough sample size, we still need more information to reach a conclusion. What we need is some measure of variability. We know that the typical person takes about 5-6 days to recover from a cold, but does everyone recover around 5-6 days, or do some people recover in 1 day, and others recover in 10 days? Understanding the spread of the data will tell us how effective the pill is. If everyone in the placebo group takes exactly 5.8 days to recover, then it is clear that the pill has a positive effect, but if people have a wide variability in their length of recovery (and they probably do) then the picture becomes a little fuzzy. Only when the mean, sample size, and variability have been calculated can a proper conclusion be made. In our case, if the sample size is large, and the variability is small, then we would receive a small p-value (probability-value). Small p-values are good, and this term is prominent enough to warrant further discussion.
In classic inferential statistics, we make two hypotheses before we start our study, the null hypothesis, and the alternative hypothesis.
Null Hypothesis: States that the two groups we are studying are the same.
Alternative Hypothesis: States that the two groups we are studying are different.
The goal in classic inferential statistics is to prove the null hypothesis wrong. The logic says that if the two groups aren't the same, then they must be different. A low p-value indicates a low probability that the null hypothesis is correct (thus, providing evidence for the alternative hypothesis).
Remember: It's good to have low p-values.
- Privacy Policy

Home » Inferential Statistics – Types, Methods and Examples
Inferential Statistics – Types, Methods and Examples
Table of Contents

Inferential Statistics
Inferential statistics is a branch of statistics that involves making predictions or inferences about a population based on a sample of data taken from that population. It is used to analyze the probabilities, assumptions, and outcomes of a hypothesis .
The basic steps of inferential statistics typically involve the following:
- Define a Hypothesis: This is often a statement about a parameter of a population, such as the population mean or population proportion.
- Select a Sample: In order to test the hypothesis, you’ll select a sample from the population. This should be done randomly and should be representative of the larger population in order to avoid bias.
- Collect Data: Once you have your sample, you’ll need to collect data. This data will be used to calculate statistics that will help you test your hypothesis.
- Perform Analysis: The collected data is then analyzed using statistical tests such as the t-test, chi-square test, or ANOVA, to name a few. These tests help to determine the likelihood that the results of your analysis occurred by chance.
- Interpret Results: The analysis can provide a probability, called a p-value, which represents the likelihood that the results occurred by chance. If this probability is below a certain level (commonly 0.05), you may reject the null hypothesis (the statement that there is no effect or relationship) in favor of the alternative hypothesis (the statement that there is an effect or relationship).
Inferential Statistics Types
Inferential statistics can be broadly categorized into two types: parametric and nonparametric. The selection of type depends on the nature of the data and the purpose of the analysis.
Parametric Inferential Statistics
These are statistical methods that assume data comes from a type of probability distribution and makes inferences about the parameters of the distribution. Common parametric methods include:
- T-tests : Used when comparing the means of two groups to see if they’re significantly different.
- Analysis of Variance (ANOVA) : Used to compare the means of more than two groups.
- Regression Analysis : Used to predict the value of one variable (dependent) based on the value of another variable (independent).
- Chi-square test for independence : Used to test if there is a significant association between two categorical variables.
- Pearson’s correlation : Used to test if there is a significant linear relationship between two continuous variables.
Nonparametric Inferential Statistics
These are methods used when the data does not meet the requirements necessary to use parametric statistics, such as when data is not normally distributed. Common nonparametric methods include:
- Mann-Whitney U Test : Non-parametric equivalent to the independent samples t-test.
- Wilcoxon Signed-Rank Test : Non-parametric equivalent to the paired samples t-test.
- Kruskal-Wallis Test : Non-parametric equivalent to the one-way ANOVA.
- Spearman’s rank correlation : Non-parametric equivalent to the Pearson correlation.
- Chi-square test for goodness of fit : Used to test if the observed frequencies for a categorical variable match the expected frequencies.
Inferential Statistics Formulas
Inferential statistics use various formulas and statistical tests to draw conclusions or make predictions about a population based on a sample from that population. Here are a few key formulas commonly used:
Confidence Interval for a Mean:
When you have a sample and want to make an inference about the population mean (µ), you might use a confidence interval.
The formula for a confidence interval around a mean is:
[Sample Mean] ± [Z-score or T-score] * (Standard Deviation / sqrt[n]) where:
- Sample Mean is the mean of your sample data
- Z-score or T-score is the value from the Z or T distribution corresponding to the desired confidence level (Z is used when the population standard deviation is known or the sample size is large, otherwise T is used)
- Standard Deviation is the standard deviation of the sample
- sqrt[n] is the square root of the sample size
Hypothesis Testing:
Hypothesis testing often involves calculating a test statistic, which is then compared to a critical value to decide whether to reject the null hypothesis.
A common test statistic for a test about a mean is the Z-score:
Z = (Sample Mean - Hypothesized Population Mean) / (Standard Deviation / sqrt[n])
where all variables are as defined above.
Chi-Square Test:
The Chi-Square Test is used when dealing with categorical data.
The formula is:
χ² = Σ [ (Observed-Expected)² / Expected ]
- Observed is the actual observed frequency
- Expected is the frequency we would expect if the null hypothesis were true
The t-test is used to compare the means of two groups. The formula for the independent samples t-test is:
t = (mean1 - mean2) / sqrt [ (sd1²/n1) + (sd2²/n2) ] where:
- mean1 and mean2 are the sample means
- sd1 and sd2 are the sample standard deviations
- n1 and n2 are the sample sizes
Inferential Statistics Examples
Sure, inferential statistics are used when making predictions or inferences about a population from a sample of data. Here are a few real-time examples:
- Medical Research: Suppose a pharmaceutical company is developing a new drug and they’re currently in the testing phase. They gather a sample of 1,000 volunteers to participate in a clinical trial. They find that 700 out of these 1,000 volunteers reported a significant reduction in their symptoms after taking the drug. Using inferential statistics, they can infer that the drug would likely be effective for the larger population.
- Customer Satisfaction: Suppose a restaurant wants to know if its customers are satisfied with their food. They could survey a sample of their customers and ask them to rate their satisfaction on a scale of 1 to 10. If the average rating was 8.5 from a sample of 200 customers, they could use inferential statistics to infer that the overall customer population is likely satisfied with the food.
- Political Polling: A polling company wants to predict who will win an upcoming presidential election. They poll a sample of 10,000 eligible voters and find that 55% prefer Candidate A, while 45% prefer Candidate B. Using inferential statistics, they infer that Candidate A has a higher likelihood of winning the election.
- E-commerce Trends: An e-commerce company wants to improve its recommendation engine. They analyze a sample of customers’ purchase history and notice a trend that customers who buy kitchen appliances also frequently buy cookbooks. They use inferential statistics to infer that recommending cookbooks to customers who buy kitchen appliances would likely increase sales.
- Public Health: A health department wants to assess the impact of a health awareness campaign on smoking rates. They survey a sample of residents before and after the campaign. If they find a significant reduction in smoking rates among the surveyed group, they can use inferential statistics to infer that the campaign likely had an impact on the larger population’s smoking habits.
Applications of Inferential Statistics
Inferential statistics are extensively used in various fields and industries to make decisions or predictions based on data. Here are some applications of inferential statistics:
- Healthcare: Inferential statistics are used in clinical trials to analyze the effect of a treatment or a drug on a sample population and then infer the likely effect on the general population. This helps in the development and approval of new treatments and drugs.
- Business: Companies use inferential statistics to understand customer behavior and preferences, market trends, and to make strategic decisions. For example, a business might sample customer satisfaction levels to infer the overall satisfaction of their customer base.
- Finance: Banks and financial institutions use inferential statistics to evaluate the risk associated with loans and investments. For example, inferential statistics can help in determining the risk of default by a borrower based on the analysis of a sample of previous borrowers with similar credit characteristics.
- Quality Control: In manufacturing, inferential statistics can be used to maintain quality standards. By analyzing a sample of the products, companies can infer the quality of all products and decide whether the manufacturing process needs adjustments.
- Social Sciences: In fields like psychology, sociology, and education, researchers use inferential statistics to draw conclusions about populations based on studies conducted on samples. For instance, a psychologist might use a survey of a sample of people to infer the prevalence of a particular psychological trait or disorder in a larger population.
- Environment Studies: Inferential statistics are also used to study and predict environmental changes and their impact. For instance, researchers might measure pollution levels in a sample of locations to infer overall pollution levels in a wider area.
- Government Policies: Governments use inferential statistics in policy-making. By analyzing sample data, they can infer the potential impacts of policies on the broader population and thus make informed decisions.
Purpose of Inferential Statistics
The purposes of inferential statistics include:
- Estimation of Population Parameters: Inferential statistics allows for the estimation of population parameters. This means that it can provide estimates about population characteristics based on sample data. For example, you might want to estimate the average weight of all men in a country by sampling a smaller group of men.
- Hypothesis Testing: Inferential statistics provides a framework for testing hypotheses. This involves making an assumption (the null hypothesis) and then testing this assumption to see if it should be rejected or not. This process enables researchers to draw conclusions about population parameters based on their sample data.
- Prediction: Inferential statistics can be used to make predictions about future outcomes. For instance, a researcher might use inferential statistics to predict the outcomes of an election or forecast sales for a company based on past data.
- Relationships Between Variables: Inferential statistics can also be used to identify relationships between variables, such as correlation or regression analysis. This can provide insights into how different factors are related to each other.
- Generalization: Inferential statistics allows researchers to generalize their findings from the sample to the larger population. It helps in making broad conclusions, given that the sample is representative of the population.
- Variability and Uncertainty: Inferential statistics also deal with the idea of uncertainty and variability in estimates and predictions. Through concepts like confidence intervals and margins of error, it provides a measure of how confident we can be in our estimations and predictions.
- Error Estimation : It provides measures of possible errors (known as margins of error), which allow us to know how much our sample results may differ from the population parameters.
Limitations of Inferential Statistics
Inferential statistics, despite its many benefits, does have some limitations. Here are some of them:
- Sampling Error : Inferential statistics are often based on the concept of sampling, where a subset of the population is used to infer about the population. There’s always a chance that the sample might not perfectly represent the population, leading to sampling errors.
- Misleading Conclusions : If assumptions for statistical tests are not met, it could lead to misleading results. This includes assumptions about the distribution of data, homogeneity of variances, independence, etc.
- False Positives and Negatives : There’s always a chance of a Type I error (rejecting a true null hypothesis, or a false positive) or a Type II error (not rejecting a false null hypothesis, or a false negative).
- Dependence on Quality of Data : The accuracy and validity of inferential statistics depend heavily on the quality of data collected. If data are biased, inaccurate, or collected using flawed methods, the results won’t be reliable.
- Limited Predictive Power : While inferential statistics can provide estimates and predictions, these are based on the current data and may not fully account for future changes or variables not included in the model.
- Complexity : Some inferential statistical methods can be quite complex and require a solid understanding of statistical principles to implement and interpret correctly.
- Influenced by Outliers : Inferential statistics can be heavily influenced by outliers. If these extreme values aren’t handled properly, they can lead to misleading results.
- Over-reliance on P-values : There’s a tendency in some fields to overly rely on p-values to determine significance, even though p-values have several limitations and are often misunderstood.
About the author
Muhammad Hassan
Researcher, Academic Writer, Web developer
You may also like

Phenomenology – Methods, Examples and Guide

Factor Analysis – Steps, Methods and Examples

Histogram – Types, Examples and Making Guide

Framework Analysis – Method, Types and Examples

Textual Analysis – Types, Examples and Guide

Methodological Framework – Types, Examples and...

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
15 Quantitative analysis: Inferential statistics
Inferential statistics are the statistical procedures that are used to reach conclusions about associations between variables. They differ from descriptive statistics in that they are explicitly designed to test hypotheses. Numerous statistical procedures fall into this category—most of which are supported by modern statistical software such as SPSS and SAS. This chapter provides a short primer on only the most basic and frequent procedures. Readers are advised to consult a formal text on statistics or take a course on statistics for more advanced procedures.
Basic concepts
British philosopher Karl Popper said that theories can never be proven, only disproven. As an example, how can we prove that the sun will rise tomorrow? Popper said that just because the sun has risen every single day that we can remember does not necessarily mean that it will rise tomorrow, because inductively derived theories are only conjectures that may or may not be predictive of future phenomena. Instead, he suggested that we may assume a theory that the sun will rise every day without necessarily proving it, and if the sun does not rise on a certain day, the theory is falsified and rejected. Likewise, we can only reject hypotheses based on contrary evidence, but can never truly accept them because the presence of evidence does not mean that we will not observe contrary evidence later. Because we cannot truly accept a hypothesis of interest (alternative hypothesis), we formulate a null hypothesis as the opposite of the alternative hypothesis, and then use empirical evidence to reject the null hypothesis to demonstrate indirect, probabilistic support for our alternative hypothesis.
A second problem with testing hypothesised relationships in social science research is that the dependent variable may be influenced by an infinite number of extraneous variables and it is not plausible to measure and control for all of these extraneous effects. Hence, even if two variables may seem to be related in an observed sample, they may not be truly related in the population, and therefore inferential statistics are never certain or deterministic, but always probabilistic.
General linear model
Most inferential statistical procedures in social science research are derived from a general family of statistical models called the general linear model (GLM). A model is an estimated mathematical equation that can be used to represent a set of data, and linear refers to a straight line. Hence, a GLM is a system of equations that can be used to represent linear patterns of relationships in observed data.
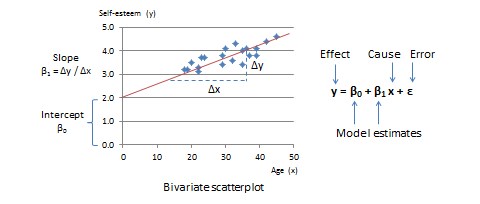
Two-group comparison
where the numerator is the difference in sample means between the treatment group (Group 1) and the control group (Group 2) and the denominator is the standard error of the difference between the two groups, which in turn, can be estimated as:
![Rendered by QuickLaTeX.com \[ s_{\overline{X}_{1}-\overline{X}_{2}} = \sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}} }\,.\]](https://usq.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-f78a6b8a224bd9fd6f3a0805214825b7_l3.png)
Factorial designs
Other quantitative analysis
There are many other useful inferential statistical techniques—based on variations in the GLM—that are briefly mentioned here. Interested readers are referred to advanced textbooks or statistics courses for more information on these techniques:
Factor analysis is a data reduction technique that is used to statistically aggregate a large number of observed measures (items) into a smaller set of unobserved (latent) variables called factors based on their underlying bivariate correlation patterns. This technique is widely used for assessment of convergent and discriminant validity in multi-item measurement scales in social science research.
Discriminant analysis is a classificatory technique that aims to place a given observation in one of several nominal categories based on a linear combination of predictor variables. The technique is similar to multiple regression, except that the dependent variable is nominal. It is popular in marketing applications, such as for classifying customers or products into categories based on salient attributes as identified from large-scale surveys.
Logistic regression (or logit model) is a GLM in which the outcome variable is binary (0 or 1) and is presumed to follow a logistic distribution, and the goal of the regression analysis is to predict the probability of the successful outcome by fitting data into a logistic curve. An example is predicting the probability of heart attack within a specific period, based on predictors such as age, body mass index, exercise regimen, and so forth. Logistic regression is extremely popular in the medical sciences. Effect size estimation is based on an ‘odds ratio’, representing the odds of an event occurring in one group versus the other.
Probit regression (or probit model) is a GLM in which the outcome variable can vary between 0 and 1—or can assume discrete values 0 and 1—and is presumed to follow a standard normal distribution, and the goal of the regression is to predict the probability of each outcome. This is a popular technique for predictive analysis in the actuarial science, financial services, insurance, and other industries for applications such as credit scoring based on a person’s credit rating, salary, debt and other information from their loan application. Probit and logit regression tend to demonstrate similar regression coefficients in comparable applications (binary outcomes), however the logit model is easier to compute and interpret.
Path analysis is a multivariate GLM technique for analysing directional relationships among a set of variables. It allows for examination of complex nomological models where the dependent variable in one equation is the independent variable in another equation, and is widely used in contemporary social science research.
Time series analysis is a technique for analysing time series data, or variables that continually changes with time. Examples of applications include forecasting stock market fluctuations and urban crime rates. This technique is popular in econometrics, mathematical finance, and signal processing. Special techniques are used to correct for autocorrelation, or correlation within values of the same variable across time.
Social Science Research: Principles, Methods and Practices (Revised edition) Copyright © 2019 by Anol Bhattacherjee is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book

Quant Analysis 101: Inferential Statistics
Everything You Need To Get Started (With Examples)
By: Derek Jansen (MBA) | Reviewers: Kerryn Warren (PhD) | October 2023
If you’re new to quantitative data analysis , one of the many terms you’re likely to hear being thrown around is inferential statistics. In this post, we’ll provide an introduction to inferential stats, using straightforward language and loads of examples .
Overview: Inferential Statistics
What are inferential statistics.
- Descriptive vs inferential statistics
Correlation
- Key takeaways
At the simplest level, inferential statistics allow you to test whether the patterns you observe in a sample are likely to be present in the population – or whether they’re just a product of chance.
In stats-speak, this “Is it real or just by chance?” assessment is known as statistical significance . We won’t go down that rabbit hole in this post, but this ability to assess statistical significance means that inferential statistics can be used to test hypotheses and in some cases, they can even be used to make predictions .
That probably sounds rather conceptual – let’s look at a practical example.
Let’s say you surveyed 100 people (this would be your sample) in a specific city about their favourite type of food. Reviewing the data, you found that 70 people selected pizza (i.e., 70% of the sample). You could then use inferential statistics to test whether that number is just due to chance , or whether it is likely representative of preferences across the entire city (this would be your population).
PS – you’d use a chi-square test for this example, but we’ll get to that a little later.

Inferential vs Descriptive
At this point, you might be wondering how inferentials differ from descriptive statistics. At the simplest level, descriptive statistics summarise and organise the data you already have (your sample), making it easier to understand.
Inferential statistics, on the other hand, allow you to use your sample data to assess whether the patterns contained within it are likely to be present in the broader population , and potentially, to make predictions about that population.
It’s example time again…
Let’s imagine you’re undertaking a study that explores shoe brand preferences among men and women. If you just wanted to identify the proportions of those who prefer different brands, you’d only require descriptive statistics .
However, if you wanted to assess whether those proportions differ between genders in the broader population (and that the difference is not just down to chance), you’d need to utilise inferential statistics .
In short, descriptive statistics describe your sample, while inferential statistics help you understand whether the patterns in your sample are likely to reflect within the population .

Let’s look at some inferential tests
Now that we’ve defined inferential statistics and explained how it differs from descriptive statistics, let’s take a look at some of the most common tests within the inferential realm . It’s worth highlighting upfront that there are many different types of inferential tests and this is most certainly not a comprehensive list – just an introductory list to get you started.
A t-test is a way to compare the means (averages) of two groups to see if they are meaningfully different, or if the difference is just by chance. In other words, to assess whether the difference is statistically significant . This is important because comparing two means side-by-side can be very misleading if one has a high variance and the other doesn’t (if this sounds like gibberish, check out our descriptive statistics post here ).
As an example, you might use a t-test to see if there’s a statistically significant difference between the exam scores of two mathematics classes taught by different teachers . This might then lead you to infer that one teacher’s teaching method is more effective than the other.
It’s worth noting that there are a few different types of t-tests . In this example, we’re referring to the independent t-test , which compares the means of two groups, as opposed to the mean of one group at different times (i.e., a paired t-test). Each of these tests has its own set of assumptions and requirements, as do all of the tests we’ll discuss here – but we’ll save assumptions for another post!

While a t-test compares the means of just two groups, an ANOVA (which stands for Analysis of Variance) can compare the means of more than two groups at once . Again, this helps you assess whether the differences in the means are statistically significant or simply a product of chance.
For example, if you want to know whether students’ test scores vary based on the type of school they attend – public, private, or homeschool – you could use ANOVA to compare the average standardised test scores of the three groups .
Similarly, you could use ANOVA to compare the average sales of a product across multiple stores. Based on this data, you could make an inference as to whether location is related to (affects) sales.
In these examples, we’re specifically referring to what’s called a one-way ANOVA , but as always, there are multiple types of ANOVAs for different applications. So, be sure to do your research before opting for any specific test.

While t-tests and ANOVAs test for differences in the means across groups, the Chi-square test is used to see if there’s a difference in the proportions of various categories . In stats speak, the Chi-square test assesses whether there’s a statistically significant relationship between two categorical variables (i.e., nominal or ordinal data). If you’re not familiar with these terms, check out our explainer video here .
As an example, you could use a Chi-square test to check if there’s a link between gender (e.g., male and female) and preference for a certain category of car (e.g., sedans or SUVs). Similarly, you could use this type of test to see if there’s a relationship between the type of breakfast people eat (cereal, toast, or nothing) and their university major (business, math or engineering).
Correlation analysis looks at the relationship between two numerical variables (like height or weight) to assess whether they “move together” in some way. In stats-speak, correlation assesses whether a statistically significant relationship exists between two variables that are interval or ratio in nature .
For example, you might find a correlation between hours spent studying and exam scores. This would suggest that generally, the more hours people spend studying, the higher their scores are likely to be.
Similarly, a correlation analysis may reveal a negative relationship between time spent watching TV and physical fitness (represented by VO2 max levels), where the more time spent in front of the television, the lower the physical fitness level.
When running a correlation analysis, you’ll be presented with a correlation coefficient (also known as an r-value), which is a number between -1 and 1. A value close to 1 means that the two variables move in the same direction , while a number close to -1 means that they move in opposite directions . A correlation value of zero means there’s no clear relationship between the two variables.
What’s important to highlight here is that while correlation analysis can help you understand how two variables are related, it doesn’t prove that one causes the other . As the adage goes, correlation is not causation.

While correlation allows you to see whether there’s a relationship between two numerical variables, regression takes it a step further by allowing you to make predictions about the value of one variable (called the dependent variable) based on the value of one or more other variables (called the independent variables).
For example, you could use regression analysis to predict house prices based on the number of bedrooms, location, and age of the house. The analysis would give you an equation that lets you plug in these factors to estimate a house’s price. Similarly, you could potentially use regression analysis to predict a person’s weight based on their height, age, and daily calorie intake.
It’s worth noting that in these examples, we’ve been talking about multiple regression , as there are multiple independent variables. While this is a popular form of regression, there are many others, including simple linear, logistic and multivariate. As always, be sure to do your research before selecting a specific statistical test.
As with correlation, keep in mind that regression analysis alone doesn’t prove causation . While it can show that variables are related and help you make predictions, it can’t prove that one variable causes another to change. Other factors that you haven’t included in your model could be influencing the results. To establish causation, you’d typically need a very specific research design that allows you to control all (or at least most) variables.
Let’s Recap
We’ve covered quite a bit of ground. Here’s a quick recap of the key takeaways:
- Inferential stats allow you to assess whether patterns in your sample are likely to be present in your population
- Some common inferential statistical tests include t-tests, ANOVA, chi-square, correlation and regression .
- Inferential statistics alone do not prove causation . To identify and measure causal relationships, you need a very specific research design.
If you’d like 1-on-1 help with your inferential statistics, check out our private coaching service , where we hold your hand throughout the quantitative research process.

Psst… there’s more!
This post is an extract from our bestselling short course, Methodology Bootcamp . If you want to work smart, you don't want to miss this .
very important content
Submit a Comment Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
- Print Friendly
Open Access is an initiative that aims to make scientific research freely available to all. To date our community has made over 100 million downloads. It’s based on principles of collaboration, unobstructed discovery, and, most importantly, scientific progression. As PhD students, we found it difficult to access the research we needed, so we decided to create a new Open Access publisher that levels the playing field for scientists across the world. How? By making research easy to access, and puts the academic needs of the researchers before the business interests of publishers.
We are a community of more than 103,000 authors and editors from 3,291 institutions spanning 160 countries, including Nobel Prize winners and some of the world’s most-cited researchers. Publishing on IntechOpen allows authors to earn citations and find new collaborators, meaning more people see your work not only from your own field of study, but from other related fields too.
Brief introduction to this section that descibes Open Access especially from an IntechOpen perspective
Want to get in touch? Contact our London head office or media team here
Our team is growing all the time, so we’re always on the lookout for smart people who want to help us reshape the world of scientific publishing.
Home > Books > Advances in Statistical Methodologies and Their Application to Real Problems
Descriptive and Inferential Statistics in Undergraduate Data Science Research Projects
Submitted: 17 April 2016 Reviewed: 12 September 2016 Published: 26 April 2017
DOI: 10.5772/65721
Cite this chapter
There are two ways to cite this chapter:
From the Edited Volume
Advances in Statistical Methodologies and Their Application to Real Problems
Edited by Tsukasa Hokimoto
To purchase hard copies of this book, please contact the representative in India: CBS Publishers & Distributors Pvt. Ltd. www.cbspd.com | [email protected]
Chapter metrics overview
2,089 Chapter Downloads
Impact of this chapter
Total Chapter Downloads on intechopen.com
Total Chapter Views on intechopen.com
Undergraduate data science research projects form an integral component of the Wesley College science and mathematics curriculum. In this chapter, we provide examples for hypothesis testing, where statistical methods or strategies are coupled with methodologies using interpolating polynomials, probability and the expected value concept in statistics. These are areas where real-world critical thinking and decision analysis applications peak a student’s interest.
- Wesley College
- undergraduate research
- phenyl chloroformate
- benzoyl chloride
- benzoyl fluoride
- benzoyl cyanide
- Grunwald-Winstein equation
- transition-state
- addition-elimination
- multiple regression
- time-series
- polynomial functions
- probability
- expected value
Author Information
Malcolm j. d’souza *.
- Department of Chemistry, Wesley College, Dover, Delaware, USA
Edward A. Brandenburg
Derald e. wentzien.
- Department of Mathematics and Data Science, Wesley College, Dover, Delaware, USA
Riza C. Bautista
Agashi p. nwogbaga, rebecca g. miller, paul e. olsen.
*Address all correspondence to: [email protected]
1. Introduction
Wesley College (Wesley) is a minority-serving, primarily undergraduate liberal-arts institution. Its STEM (science, technology, engineering and mathematics) fields contain a robust (federal and state) sponsored directed research program [ 1 , 2 ]. In this program, students receive individual mentoring on diverse projects from a full-time STEM faculty member. In addition, undergraduate research is a capstone thesis requirement and students complete research projects within experiential courses or for an annual Scholars’ Day event.
Undergraduate research is indeed a hallmark of Wesley’s progressive liberal-arts core-curriculum. All incoming freshmen are immersed in research in a specially designed quantitative reasoning a 100-level mathematics core course, a first-year seminar course and 100-level frontiers in science core course [ 1 ]. Projects in all level-1 STEM core courses provide an opportunity to develop a base knowledge for interacting and manipulating data. These courses also introduce students to modern computing techniques and platforms.
At the other end of the Wesley core-curriculum spectrum, the advanced undergraduate STEM research requirements reflect the breadth and rigor necessary to prepare students for (possible) future postgraduate programs. For analyzing data in experiential research projects, descriptive and inferential statistics are major components. In informatics, students are trained in the SAS Institute’s statistical analysis system (SAS) software and in the use of geographic information system (GIS) spatial tools through ESRI’s ArcGIS platform [ 2 ].
To help students with poor mathematical ability and to further enhance their general thinking skills, in our remedial mathematics courses, we provide a foundation in algebraic concepts, problem-solving skills, basic quantitative reasoning and simple simulations. Our institution also provides a plethora of student academic support services that include an early alert system, peer and professionally trained tutoring services and writing center support. In addition, Wesley College non-STEM majors are required to take the project-based 100-level mathematics core course and can then opt to take two project-based 300-level SAS and GIS core courses. Such students who are trained in the concepts and applications of mathematical and statistical methods can then participate in Scholars’ Day to augment their mathematical and critical thinking skills.
2. Linear free energy relationships to understand molecular pathways
Single and multiparameter linear free energy relationships (LFERs) help chemists evaluate multiple kinds of transition-state molecular interactions observed in association with compound variability [ 3 ]. Chemical kinetics measurements are understood by correlating the experimental compound reaction rate ( k ) or equilibrium data and their thermodynamics. The computationally challenging stoichiometric analysis elucidates metabolic pathways by analyzing the effect of physiochemical, environmental and biological factors on the overall chemical network structure. All of these determinations are important in the design of chemical processes for petrochemical, pharmaceutical and agricultural building blocks.
In this section, through results obtained from our undergraduate directed research program in chemistry, we outline examples with statistical descriptors that use inferential correctness for testing hypotheses about regression coefficients in LFERs that are common to the study of solvent reactions. To understand mechanistic approaches, multiple regression correlation analyses using the one- and two-term Grunwald-Winstein equations (Eqs. ( 1 ) and ( 2 )) are proven to be effective instruments that elucidate the transition-state in solvolytic reactions [ 3 ]. To avoid multicollinearity, it is stressed that the chosen solvents have widely varying ranges of nucleophilicity ( N ) and solvent-ionizing power ( Y ) values [ 3 , 4 ]. In Eqs. ( 1 ) and ( 2 ) (for a particular substrate), k is the rate of reaction in a given solvent, k o is the 80% ethanol (EtOH) reaction rate, l is the sensitivity toward changes in N, m is the sensitivity toward changes in Y and c is a constant (residual) term. In substrates that have the potential for transition-state electron delocalization, Kevill and D’Souza introduced an additional hI term to Eqs. ( 1 ) and ( 2 ) (and as shown in Eqs. ( 3 ) and ( 4 )). In Eqs. ( 3 ) and ( 4 ), h represents the sensitivity to changes in the aromatic ring parameter I [ 3 ].
Eqs. ( 1 ) and ( 3 ) are useful in substrates where the unimolecular dissociative transition-state (S N 1 or E1) formation is rate-determining. Eqs. ( 2 ) and ( 4 ) are employed for reactions where there is evidence for bimolecular associative (S N 2 or E2) mechanisms or addition-elimination (A-E) processes. In substrates undergoing similar mechanisms, the resultant l / m ratios obtained can be important indicators to compensate for earlier and later transition-states (TS). Furthermore, l / m ratios between 0.5 and 1.0 are indicative of unimolecular processes (S N 1 or E1), values ≥ 2.0 are typical in bimolecular processes (S N 2, E2, or A-E mechanisms) and values <<0.5 imply that ionization-fragmentation is occurring [ 3 ].
To study the (solvent) nucleophilic attack at a sp 2 carbonyl carbon, we completed detailed Grunwald-Winstein (Eqs. ( 1 ), ( 2 ) and ( 4 )) analyses for phenyl chloroformate (PhOCOCl) at 25.0°C in 49 solvents with widely varying N and Y values [ 3 , 4 ]. Using Eq. ( 1 ), we obtained an m value of −0.07 ± 0.11, c = −0.46 ± 0.31, a very poor correlation coefficient ( R = 0.093) and an extremely low F -test value of 0.4. An analysis of Eq. ( 2 ) resulted in a very robust correlation, with R = 0.980, F -test = 568, l = 1.66 ± 0.05, m = 0.56 ± 0.03 and c = 0.15 ± 0.07. Using Eq. ( 4 ), we obtained l = 1.77 ± 0.08, m = 0.61 ± 0.04, h = 0.35 ± 0.19 ( P -value = 0.07), c = 0.16 ± 0.06, R = 0.982 and the F -test value was 400.
Since the use of Eq. ( 2 ) provided superior statistically significant results ( R, F -test and P -values) for PhOCOCl, we strongly recommended that in substrates where nucleophilic attack occurs at a sp 2 hybridized carbonyl carbon, the PhOCOCl l / m ratio of 2.96 should be used as a guiding indicator for determining the presence of an addition-elimination (A-E) process [ 3 , 4 ]. Furthermore, for n -octyl fluoroformate (OctOCOF) and n -octyl chloroformate (OctOCOCl), we found that the leaving-group ratio ( k F / k Cl ) was close to, or above unity. Fluorine is a very poor leaving-group when compared to chlorine, hence for carbonyl group containing molecules, we proposed the existence of a bimolecular tetrahedral transition-state (TS) with a rate-determining addition step within an A-E pathway (as opposed to a bimolecular concerted associative S N 2 process with a penta-coordinate TS).
For chemoselectivity, the sp 2 hybridized benzoyl groups (PhCO─) are found to be efficient and practical protecting agents that are utilized during the synthesis of nucleoside, nucleotide and oligonucleotide analogue derivative compounds. Yields for regio- and stereoselective reactions are shown to depend on the preference of the leaving group and commercially, benzoyl fluoride (PhCOF), benzoyl chloride (PhCOCl) and benzoyl cyanide (PhCOCN) are cheap and readily available.
We experimentally measured the solvolytic rates for PhCOF at 25.0°C [ 5 ]. In 37 solvent systems, a two-term Grunwald-Winstein (Eq. ( 2 )) application resulted in an l value of 1.58 ± 0.09, an m value of 0.82 ± 0.05, a c value of −0.09, R = 0.953 and the F -test value was 186. The l / m ratio of 1.93 for PhCOF is close to the OctOCOF l / m ratio of 2.28 (in 28 pure and binary mixtures) indicating similar A-E transition states with rate-determining addition.
On the other hand, for PhCOCl at 25.0°C, we used the available literature data (47 solvents) from various international groups and proved the presence of simultaneous competing dual side-by-side mechanisms [ 6 ]. For 32 of the more ionizing solvents, we obtained l = 0.47 ± 0.03, m = 0.79 ± 0.02, c = −0.49 ± 0.17, R = 0.990 and F -test = 680. The l / m ratio is 0.59. Hence, we proposed an S N 1 process with significant solvation ( l component) of the developing aryl acylium ion. In 12 of the more nucleophilic solvents, we obtained l = 1.27 ± 0.29, m = 0.46 ± 0.07, c = 0.18 ± 0.23, R = 0.917 and F -test = 24. The l / m ratio of 2.76 is close to the 2.96 value obtained for PhOCOCl. This suggests that the A-E pathway is prevalent. In addition, there were three solvents where there was no clear demarcation of the changeover region.
At 25.0°C in solvents that are common to PhCOCl and PhCOCF we observed k PhCOCl > k PhCOF . This rate trend is primarily due to more efficient PhCOF ground-state stabilization.
Lee and co-workers followed the kinetics of benzoyl cyanide (PhCOCN) at 1, 5, 10, 15 and 20°C in a variety of pure and mixed solvents and proposed the presence of an associative S N 2 (penta-coordinate TS) process [ 7 ]. PhCOCN is an ecologically important chemical defensive secretion of polydesmoid millipedes and cyanide is a synthetically useful highly active leaving group. Since the leaving group is involved in the rate-determining step of any S N 2 process, we became skeptical with the associative S N 2 proposal and decided to reinvestigate the PhCOCN analysis. We hypothesized that since PhCOCl showed mechanism duality, similar analogous dual mechanisms should endure during PhCOCN solvolyses.
Using the Lee data within Arrhenius plots (Eq. ( 5 )), we determined the PhCOCN solvolytic rates at 25°C ( Table 1 ). We obtained the rates for PhCOCN in 39 pure and mixed
| Solvent (v/v) | 10 k/s | Solvent (v/v) | 10 k/s | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 139.9 | 0.16 | −0.94 | 0.10 | 2447 | −0.96 | 3.21 | −0.38 | ||
| 210.0 | 0.00 | 0.00 | 0.00 | 3726 | −1.11 | 3.77 | −0.40 | ||
| 322.8 | −0.20 | 0.78 | −0.06 | 4071 | −1.23 | 4.28 | −0.43 | ||
| 598.8 | −0.38 | 1.38 | −0.15 | 1690 | −0.98 | 2.97 | −0.29 | ||
| 986.7 | −0.58 | 2.02 | −0.23 | 2887 | −1.12 | 3.71 | −0.25 | ||
| 1761 | −0.74 | 2.75 | −0.24 | 4196 | −1.25 | 4.23 | −0.34 | ||
| 3064 | −0.93 | 3.53 | −0.30 | 37.20 | 0.27 | −1.99 | 0.26 | ||
| 3732 | −1.16 | 4.09 | −0.33 | 41.64 | 0.08 | −1.42 | 0.31 | ||
| 390.5 | −0.01 | −0.18 | 0.28 | 35.50 | −0.11 | −0.95 | 0.38 | ||
| 575.3 | −0.06 | 0.67 | 0.14 | 32.98 | −0.34 | −0.48 | 0.43 | ||
| 800.2 | −0.40 | 1.46 | 0.04 | 30.30 | −0.64 | 0.16 | 0.51 | ||
| 1616 | −0.54 | 2.07 | −0.19 | 27.70 | −1.34 | 1.24 | 0.65 | ||
| 2573 | −0.75 | 2.70 | −0.05 | 639.9 | −2.19 | 2.84 | 0.28 | ||
| 4205 | −0.87 | 3.25 | −0.13 | 886.1 | −1.88 | 2.93 | 0.22 | ||
| 5351 | −1.06 | 3.73 | −0.22 | 1075 | −1.78 | 3.05 | 0.14 | ||
| 9.547 | −0.37 | −0.83 | −0.23 | 1512 | −1.33 | 3.21 | 0.06 | ||
| 86.02 | −0.42 | 0.17 | −0.29 | 2089 | −1.19 | 3.44 | −0.03 | ||
| 157.1 | −0.52 | 0.95 | −0.28 | 2944 | −1.15 | 3.73 | −0.15 | ||
| 505.9 | −0.70 | 1.73 | −0.32 | 3870 | −1.23 | 4.10 | −0.29 | ||
| 1149 | −0.83 | 2.46 | −0.35 | – | – | – | – | – |
The 25.0°C calculated rates for PhCOCN, the N T , Y Cl and I values.
1 Calculated using four data points in an Arrhenius plot.
2 Calculated using three data points in an Arrhenius plot.
3 Calculated using three data points in an Arrhenius plot and are w/w compositions.
4 Determined using a second-degree polynomial equation.
5 Determined using a third-degree polynomial equation.
aqueous organic solvents of ethanol (EtOH), methanol (MeOH), acetone (Me 2 CO), dioxane, 2,2,2-trifluoroethanol (TFE) and in TFE-EtOH (T-E) mixtures. For all of the Arrhenius plots, the R 2 values ranged from 0.9937 to 1.0000, except in 60% Me 2 CO, R 2 was 0.9861. The Arrhenius plot for 80% EtOH is shown in Figure 1 . In order to utilize Eqs. ( 1 )–( 4 ) for all 39 solvents, second degree or third-degree polynomial equations were used to calculate the missing N T , Y Cl and I values. The calculated 25°C PhCOCN reaction rates and the literature available or interpolated N T , Y Cl and I values are listed in Table 1 .
Using Eq. ( 2 ) for 32 of the PhCOCN solvents in Table 1 (20–90% EtOH, 30–90% MeOH, 20–80% Me 2 CO, 10–30% dioxane, 10T–90E, 20T–80E, 30T–70E, 40T–60E, 50T–50E and 70T–30E), we obtained R = 0.988, F -test = 595, l = 1.54 ± 0.11, m = 0.74 ± 0.03 and c = 0.13 ± 0.04. Using Eq. ( 4 ), we obtained R = 0.989, F -test = 432, l = 1.62 ± 0.11, m = 0.78 ± 0.03, h = 0.22 ± 0.11 ( P -value = 0.07) and c = 0.13 ± 0.04.

Arrhenius plot for 80% EtOH.
The l / m ratio of 2.08 obtained (for PhCOCN) using Eq. ( 2 ) is close to that obtained (1.93) for PhCOF and hence we propose a parallel A-E mechanism.
For the seven highly ionizing aqueous TFE mixtures, using Eq. ( 1 ) we obtained, R = 0.977, F -test = 105, m = 0.61 ± 0.06 and c = −1.15 ± 0.20. Using Eq. ( 2 ) we obtained R = 0.999, F -test = 763, l = 0.25 ± 0.031, m = 0.42 ± 0.03 and c = −0.13 ± 0.14. Using Eqs. ( 3 ) and ( 4 ) we obtained R = 0.998, F -test = 417, m = −0.65 ± 0.22 ( P -value = 0.04), h = −2.83 ± 0.491 ( P -value = 0.01) and c = 3.12 ± 0.73 ( P -value = 0.01) and R = 0.989, F -test = 572, l = 0.17 ± 0.07 ( P -value = 0.11), m = 0.02 ± 0.33 ( P -value = 0.96), h = −1.04 ± 0.86 ( P -value = 0.31), c = 1.10 ± 1.02 ( P -value = 0.36), respectively.
In the very polar TFE mixtures, in Eq. ( 2 ) the l / m ratio was 0.60, indicating a dissociative S N 1 process. The l value of 0.25 is consistent with the need of small preferential solvation to stabilize the developing S N 1 carbocation and the lower m value (0.42) attained can be rationalized in terms of less demand for solvation of the cyanide anion (leaving group).
In all of the common solvents at 25.0°C, k PhCOCl > k PhCOCN > k PhCOF . In addition, PhCOCN was found to be faster than PhCOF by a factor of 18–71 times in the aqueous ethanol, methanol, acetone and dioxane mixtures and 185–1100 times faster in the TFE-EtOH and TFE-H 2 O mixtures. These observations are very reasonable as the cyanide group is shown to have a greater inductive effect and in addition, the cyanide anion is a weak conjugate base. This rationalization is logical as ( l / m ) PhCOCN > ( l / m ) PhCOF .
3. Estimating missing values from a time series data set
Complete historical data time series are needed to create effective mathematical models. Unfortunately, systems that track and record the data values periodically malfunction thereby creating missing and/or inaccurate values in the time series. If a reasonable estimate for the missing value can be determined, the data series can then be used for future analysis.
In this section, we present a methodology to generate a reasonable estimate for a missing or inaccurate values when two important conditions exist: (1) a similar data series with complete information is available and (2) a pattern (or trend) is observable.
The extent of the ice at the northern polar ice cap in square kilometers is tracked on a daily basis and this data is made available to researchers by the National Snow & Ice Data Center (NSIDC). A review of the NASA Distributed Active Archive Center (DAAC) data at NSIDC indicates that the extent of the northern polar ice cap follows a cyclical pattern throughout the year. The extent increases until it reaches a maximum for the year in mid-March and decreases until it reaches a minimum for the year in mid-September. Unfortunately, the data set contains missing data for some of the days.
The extent of the northern polar ice cap in the month of January for 2011, 2012 and 2013 is utilized as an example. Complete daily data for January in 2011 and 2012 is available. The 2013 January data has a missing data value for January 25, 2013.
Figure 2 presents the line graph of the daily ice extent for January of 2011, 2012 and 2013. A complete time series is available for 2011 and 2012, so the first condition is met. The line graphs also indicate that the extent of the polar ice caps is increasing in January, so the second condition is met. An interpolating polynomial will be introduced and used to estimate the missing value for the extent of the polar ice cap on January 25, 2013.
Let t = the time period or observation number in a time series.
Let f ( t) = the extent of the sea ice for time period t .
The extent of the sea ice can be written as a function of time.
For a polynomial of degree 1, the function will be: f ( t ) = a 0 + a 1 ( t )
For a polynomial of degree 3, the function will be: f ( t ) = a 0 + a 1 ( t ) + a 2 ( t ) 2 + a 3 ( t ) 3
Polynomials of higher degrees could also be used. The extent of the polar ice for January 25 will be removed from the data series for 2011 and 2012 and an estimate will be prepared using polynomials of degree 1. Another estimate is prepared using polynomials of degree 3. The estimated value will be compared to the actual value for the years 2011 and 2012. The degree of the polynomial that generates the best (closest) estimate for January 25 will be the degree of the polynomial used to generate the estimate for January 25, 2013.

The extent of sea ice in January 2011, 2012 and 2013.
A two-equation, two-unknown system of equations is created when using polynomials of degree 1. One known value before and after the missing value for each year is used to set up the system of equations. To simplify the calculations, January 24 is recorded as time period 1, January 25 is recorded as time period 2 and January 26 is recorded as time period 3. The time period and extent of the sea ice for each year was recorded in Excel.
| Time period | 2011 | 2012 | 2013 |
| 1 | 12,878,750 | 13,110,000 | 13,077,813 |
| 2 | 12,916,563 | 13,123,125 | |
| 3 | 12,996,875 | 13,204,219 | 13,404,688 |
The system of equations using a first-order polynomial for January 2011 is:
The coefficients a i can be found by solving the system of equations. Substitution, elimination, or matrices can be used to solve the system of equations. A TI-84 graphing calculator and matrices were used to solve this system.
The solution to this system of equations is: a 0 = 12 , 819 , 687.5 , a 1 = 59 , 062.5
The estimate for January 25, 2011 is: 12 , 819 , 687.5 + 59 , 062.2 ( 2 ) = 12 , 937 , 812.5 km 2 .
The system of equations using a first-order polynomial for 2012 is:
The solution to this system of equations is: a 0 = 13 , 062 , 890.5 , a 1 = 47 , 109.5
The estimate for January 25, 2012 is: 13 , 062 , 890.5 + 47 , 109.5 ( 2 ) = 13 , 157 , 109.5 km 2 .
The absolute values of the deviations (actual and estimated values) were calculated in Excel.
| Degree | Year | Actual | Estimated | Absolute deviation |
| 1 | 2011 | 12,916,563 | 12,937,812.5 | 21,249.5 |
| 1 | 2012 | 13,123,125 | 13,157,109.5 | 33,984.5 |
A four-equation, four-unknown system of equations is created when using polynomials of degree 3. Two known values before and after the missing value are used to set up the system of equations. To simplify the calculations, January 23 is recorded as time period 1, January 24 is recorded as time period 2, January 25 is recorded as time period 3, January 26 is recorded as time period 4 and January 27 is recorded as time period 5. The time period and extent of the sea ice for each year was recorded in Excel.
| Time period | 2011 | 2012 | 2013 |
| 1 | 12,848,281 | 13,199,375 | 13,168,594 |
| 2 | 12,878,750 | 13,110,000 | 13,077,813 |
| 3 | 12,916,563 | 13,123,125 | |
| 4 | 12,996,875 | 13,204,219 | 13,404,688 |
| 5 | 13,090,625 | 13,227,344 | 13,388,750 |
The system of equations using a third-order polynomial for 2011 is:
The solution to this system of equations is: a 0 = 12 , 832 , 811.67 , a 1 = 8 , 985.17 , a 2 = 5 , 976.33 , a 3 = 507.83
The estimate for January 25, 2011 is: 12 , 832 , 811.67 + 8 , 985.17 ( 3 ) + 5 , 976.33 ( 3 ) 2 + 507.33 ( 3 ) 3 = 12 , 927 , 252.1 km 2 .
The system of equations using a third-order polynomial for 2012 is:
The solution to this system of equations is: a 0 = 13 , 486 , 719 , a 1 = − 413 , 073.33 , a 2 = 139 , 101.75 , a 3 = − 13 , 372.42
The estimate for January 25, 2012 is: 13 , 486 , 719 − 413 , 073.33 ( 3 ) + 139 , 101.75 ( 3 ) 2 − 13 , 372.42 ( 3 ) 3 = 13 , 138 , 359.42 km 2
| Degree | Year | Actual | Estimated | Absolute deviation |
| 3 | 2011 | 12,916,563 | 12,927,252.1 | 10,689.1 |
| 3 | 2012 | 13,123,125 | 13,138,359.4 | 15,234.4 |
The mean of the absolute deviations for polynomials of degree 1 and the mean of the absolute deviations for polynomials of degree 3 were calculated in Excel. The polynomial of degree 3 provided the smallest mean absolute deviation.
| Degree | Mean absolute deviation |
| 1 | 27,617.00 |
| 3 | 12,961.75 |
Therefore, a third order polynomial will be used to generate an estimate for the sea ice extent on January 25, 2013.
The system of equations using a third-order polynomial for 2013 is:
The solution to this system of equations is: a 0 = 13 , 717 , 916.67 , a 1 = − 850 , 859.17 , a 2 = 337 , 669.33 , a 3 = − 36 , 132.83 .
The estimate for January 25, 2013 is: 13 , 717 , 916.67 − 850 , 859.17 ( 3 ) + 337 , 669.33 ( 3 ) 2 − 36 , 132.83 ( 3 ) 3 = 13 , 228 , 776.72 km 2 . Figure 3 shows the extent of the sea ice in January, 2013 with the estimate for January 25.

The extent of sea ice in January 2013 with the January 25, 2013 estimate.
4. Statistical methodologies and applications in the Ebola war
In 2014, an unprecedented outbreak of Ebola occurred predominantly in West Africa. According to the Center for Disease Control (CDC), over 28.5 thousand cases were reported resulting in more than 11,000 deaths [ 8 ]. The countries that were affected by the Ebola outbreak were Senegal, Guinea, Nigeria, Mali, Sierra Leone, Liberia, Spain and the United States of America (USA). Statistics through dynamic modeling played a crucial role with clinical data collection and management. The lessons learned and the resultant statistical advances continue to inform and drive current and subsequent pandemics.
For this honors thesis project, we tracked and gathered Ebola data over an extended period of time from the CDC, World Health Organization (WHO) and the news media [ 8 , 9 ]. We used statistical curve fitting that involved both exponential and polynomial functions as well as model validation using nonlinear regression and R 2 statistical analysis.
The first WHO report (initial announcement) of the West Africa Ebola outbreak was made during the March 23rd, 2014 week. Consequently, the data for this project began from that week to October 31, 2014. The 2014 Ebola data was used to create epidemiological models to predict the possible pathway of a 2014 West Africa type of Ebola outbreak. The WHO number of Ebola cases and death toll as of October 31st, 2014 were Liberia (6635 cases with 2413 deaths), Sierra Leone (5338 cases with 1510 deaths), Guinea (1667 cases with 1018 deaths), Nigeria (20 cases with eight deaths), the United States (four cases with one death), Mali (one case with one death) and Spain (one case with zero death).
Microsoft Excel was used for the modeling of the three examples shown and were predicated upon the following assumptions: (1) Week 1 is the week of March 23rd, 2014; (2) X is the number of weeks starting from Week 1 and Y is the number of Ebola deaths; (3) there was no vaccine/cure; and (4) the missing data for the 24th week was obtained by interpolation.
4.1. Modeling of weekly Guinea Ebola deaths
The dotted curve in Figure 4 shows the actual observed deaths while the solid line shows the number of deaths as determined by the fitted model. As shown in Figure 4 , the growth of the Guinea deaths is exponential. The best fit curve for the projected growth is y = 72.827e 0.0823 x . A comparison of the actual data to the projected data shows that the two are similar but not exact ( Table 2 ). The projected amount of deaths is approximately 1300 by week 35 (or the week of November 23, 2014).
4.2. Modeling of Liberia Ebola deaths (weekly)
Unlike the Guinea deaths, the Liberian deaths are modeled using polynomial function ( Figure 5 ).

Weekly deaths in Guinea.
| Ebola deaths in Guinea | ||||||||
|---|---|---|---|---|---|---|---|---|
| Week | Deaths | Model | Week | Deaths | Model | Week | Deaths | Model |
| 1 | 29 | 79 | 13 | 264 | 212 | 25 | 494 | 570 |
| 2 | 70 | 86 | 14 | 267 | 231 | 26 | 494 | 619 |
| 3 | 95 | 93 | 15 | 303 | 250 | 27 | 648 | 672 |
| 4 | 108 | 101 | 16 | 307 | 272 | 28 | 739 | 730 |
| 5 | 136 | 110 | 17 | 304 | 295 | 29 | 862 | 792 |
| 6 | 143 | 119 | 18 | 314 | 320 | 30 | 904 | 860 |
| 7 | 155 | 130 | 19 | 339 | 348 | 31 | XXX | 934 |
| 8 | 157 | 141 | 20 | 363 | 378 | 32 | XXX | 1014 |
| 9 | 174 | 153 | 21 | 377 | 410 | 33 | XXX | 1101 |
| 10 | 193 | 166 | 22 | 396 | 445 | 34 | XXX | 1195 |
| 11 | 215 | 180 | 23 | 406 | 483 | 35 | XXX | 1298 |
| 12 | 226 | 196 | 24 | 450 | 525 | 36 | XXX | XXX |
Actual and projected Ebola deaths in Guinea.
The best fit curve is best defined with the polynomial equation y = 0.0003 x 5 − 0.0069 x 4 + 0.0347 x 3 + 0.5074 x 2 − 4.1442 x + 10.487. The model is not exact but it is close enough to predict that by week 35, there would be over 7000 deaths in Liberia ( Table 3 ).

Weekly deaths in Liberia.
| Ebola deaths in Liberia | ||||||||
|---|---|---|---|---|---|---|---|---|
| Week | Deaths | Model | Week | Deaths | Model | Week | Deaths | Model |
| 1 | 0 | 7 | 13 | 24 | 33 | 25 | 871 | 1001 |
| 2 | 0 | 4 | 14 | 25 | 43 | 26 | 670 | 1267 |
| 3 | 10 | 3 | 15 | 65 | 58 | 27 | 1830 | 1589 |
| 4 | 13 | 3 | 16 | 84 | 79 | 28 | 2069 | 1976 |
| 5 | 6 | 3 | 17 | 105 | 107 | 29 | 2484 | 2436 |
| 6 | 6 | 5 | 18 | 127 | 145 | 30 | 2705 | 2981 |
| 7 | 11 | 7 | 19 | 156 | 197 | 31 | XXX | 3620 |
| 8 | 11 | 9 | 20 | 282 | 264 | 32 | XXX | 4366 |
| 9 | 11 | 12 | 21 | 355 | 352 | 33 | XXX | 5231 |
| 10 | 11 | 15 | 22 | 576 | 464 | 34 | XXX | 6230 |
| 11 | 11 | 20 | 23 | 624 | 606 | 35 | XXX | 7377 |
| 12 | 11 | 25 | 24 | 748 | 783 | 36 | XXX | XXX |
Actual and projected Ebola deaths in Liberia.
4.3. Modeling of total deaths (World)
When analyzing the total deaths of Ebola (for 35 weeks), the data was best modeled using the polynomial function y = 0.033 x 4 − 1.4617 x 3 + 23.437 x 2 − 118.18 x + 231.59 ( Figure 6 ). An exponential function was not used as it was not suitable since the actual growth was not (initially) fast enough to match the exponential growth. As shown in Table 4 , the projected total deaths according to this model would be greater than 11,000 by week 35.

Weekly world-wide deaths.
| Total Ebola deaths in the world | ||||||||
|---|---|---|---|---|---|---|---|---|
| Week | Deaths | Model | Week | Deaths | Model | Week | Deaths | Model |
| 1 | 29 | 135 | 13 | 337 | 387 | 25 | 1848 | 1977 |
| 2 | 70 | 78 | 14 | 350 | 428 | 26 | 1647 | 2392 |
| 3 | 105 | 51 | 15 | 467 | 470 | 27 | 3091 | 2893 |
| 4 | 121 | 49 | 16 | 518 | 516 | 28 | 3439 | 3494 |
| 5 | 142 | 65 | 17 | 603 | 571 | 29 | 4555 | 4206 |
| 6 | 149 | 93 | 18 | 660 | 638 | 30 | 4877 | 5044 |
| 7 | 166 | 131 | 19 | 729 | 722 | 31 | XXX | 6022 |
| 8 | 168 | 173 | 20 | 932 | 829 | 32 | XXX | 7155 |
| 9 | 185 | 217 | 21 | 1069 | 967 | 33 | XXX | 8461 |
| 10 | 210 | 262 | 22 | 1350 | 1141 | 34 | XXX | 9955 |
| 11 | 232 | 305 | 23 | 1427 | 1362 | 35 | XXX | 11656 |
| 12 | 244 | 347 | 24 | 1638 | 1637 | 36 | XXX | XXX |
Actual and projected worldwide deaths.
4.4. Nonlinear regression and R -squared analysis
A visual inspection of the graphs and tables shows that the model for Liberia as well as the model for the world-wide total deaths evidently fits the data more closely and a lot better than does the Guinea model. Hence, other statistical goodness-of-fit tests are used to reassert these observations. Here, nonlinear polynomial regression (Eq. ( 11 )) and R 2 statistical analysis are employed. In Eq. ( 11 ), Σ signifies summation, w refers to the actual (observed) number of Ebola deaths, z is the number of Ebola deaths as calculated with the model and n is the total number of weeks.
For the Guinea epidemiological Ebola model, the nonlinear regression equation is y = 72.827e 0.0823x with R 2 as 0.9077 indicating that about 91% of the total variations in y (the number of actual Ebola deaths) can be explained by the regression equation. The polynomial epidemiological model for Ebola deaths in Liberia, y = 0.0003 x 5 − 0.0069 x 4 + 0.0347 x 3 + 0.5074 x 2 − 4.1442 x + 10.487, has R 2 as 0.9715 so that about 97% of the total variations in y (the number of observed Ebola deaths) can be explained by the regression equation. For the third world-wide model, the polynomial for the total Ebola deaths for all countries combined is expectedly better. Here, the R 2 is 0.9823, so that about 98% of the total variations in the number of actual Ebola deaths can be explained by the regression equation, y = 0.033 x 4 − 1.4617 x 3 + 23.437 x 2 − 118.18 x + 231.59.
This shows that recording good and organized data that is easily retrievable is paramount in the fight of pandemics. The statistical models developed, in turn, can continue to inform and drive current and subsequent pandemic analyses.
5. Probability and expected value in statistics
At Wesley College, probability and expected value in statistics are introduced in two freshman-level mathematics classes: the quantitative reasoning math-core course and a first-year seminar, Mathematics in Gambling .
In general, there are two practical approaches to assigning a probability value to an event:
The classical approach
The relative frequency/empirical approach and
The classical approach to assigning a probability assumes that all outcomes to a probability experiment are equally likely. In the case of a roulette wheel at a casino, the little rolling ball is equally likely to land in any of the 38 compartments of the roulette wheel. In general, the rule for the probability of an event according to the classical approach is:
In the case of roulette, the probability an individual wins by placing a bet on the color red is 18/38. Since there are 18 red, 18 black and 2 green compartments, the probability of a gambler winning by placing a bet on the color red is 18 38 = 9 19 or approximately 0.474.
Unfortunately, the classical approach to probability is not always applicable. In the insurance industry, actuaries are interested in the likelihood of a policyholder dying. Since the two events of a policyholder living or dying are not equally likely, the classical approach cannot be used.
Instead, the relative frequency approach is used, which is:
When setting life insurance rates for policyholders, life insurance companies must consider variables such as age, sex and smoking status (among others). Suppose recent mortality data for 65-year-old non-smoking males indicates 1800 such men died last year out of 900,000 such men. Based on this data, one would say the probability a 65-year-old non-smoking male will die in the next year, based on the relative frequency approach is:
P (65-year-old non-smoking male dies) = 1 , 800 900 , 000 or approximately 0.002 or 0.2%.
The field of decision analysis often employs the concept of expected value . Take the case of a 65-year-old non-smoking male buying a $250,000 term life insurance policy. Is it worth buying this policy? Based on the concept of expected value, a calculation based on probability is made and interpreted. If the value turns out to be negative, students then have to explain the rationale justifying the purpose of purchasing the term life insurance policy.
For a casino installing, a roulette wheel or craps table will the table game be a money maker for the casino? In the Mathematics of Gambling first-year seminar course, students research the rules for the game of roulette and the payoffs for various bets. Based on their findings, they determine the “house edge” for various bets. They also compare various bets in different games of chance to analyze which is a “better bet” and in what game.
Assume a situation has various outcomes/states of nature which occur randomly and are unknown when a decision is to be made. In the case of a person considering a life-insurance policy, the person will either live (L) or die (D) during the next year. Assuming the person has no adverse medical condition, the person’s state of nature is unknown when he has to make the decision to buy the term life-insurance (the two outcomes will occur in no predictable manner and are considered random). If each monetary outcome (denoted O i ) has a probability (denoted p i ), then the expected value can be computed by the formula:
where there are n possible outcomes.
In other words, it is the sum of each monetary outcome times its corresponding probability.
Example 1: A freshman-level quantitative reasoning mathematics-core class
Assume a 67-year-old non-smoking male is charged $1180 for a one year $250,000 term life-insurance policy. Assume actuarial tables show the probability of death for such a person to be 0.003. What is the expected value of this life-insurance policy to the buyer?
A payoff table can be constructed showing the outcomes, probabilities and “net” payoffs:
| Outcome: | ||
| Probability: | 0.003 | 1 – 0.003 = 0.997 |
| Net payoff: | $250,000–$1180 | |
| $248,820 |
The payoff in the case of the person living is negative since the money is spent with no return on the investment. Using these data, the expected value is calculated as
The negative sign in the expected value means the consumer should expect to lose money (while the insurance company can expect to make money). Students are asked to explain the meaning of the expected value and explain reasons for people throwing their money away like this. What will they do when it comes time to consider term life insurance?
Example 2: Mathematics of Gambling class
Students are asked to research rules of various games of chance, the meaning of various payoffs (for example, 35 to 1 versus 35 for 1) and then be asked to calculate and interpret the house edge in gambling. This is defined by the formula
By asking different students to evaluate the house edge of different gambling bets, students can analyze and decide which bet is safest if they do choose to gamble.
Which bet has the lower house edge and why?
Bet #1 – Placing a $10 bet in American roulette on the “row” 25– 27.
Bet #2 – Placing a $5 bet in Craps on rolling the sum of 11.
Students must research each game of chance and determine important information to use, which is recorded as follows:
| $10 Bet on a row in roulette | $5 Bet on a sum of 11 in craps | |
| Probability of a winning bet: | ||
| Payoff odds: | 11 to 1 | 15 to 1 |
| Payoff: | −$110 | −$75 |
| Probability of a losing bet: | ||
| Payoff to house for lost bet: | +$5 | |
| House Edge: | $0.0526 | $0.1111 |
| Computed by: |
The roulette bet has a lower house edge and is financially safer in the long run for the gambler. Students were then asked to compute the house edge using the shortcut method based on the theory of odds. The house edge is the difference between the true odds (denoted a:b ) and the payoff odds the casino pays, expressed as a percentage of the true total odds ( a + b ).
In the example involving craps, the true odds against a sum of 11 is 34:2 which reduces to 17:1. The difference between the true odds and payoff odds is 17 – 15 (see Example 2) = 2. Expressing this difference as a percentage of (a + b), the house edge is then calculated as 2 ÷ ( 17 + 1 ) = 2 ÷ 18 = 1 9 = 0.1111 which is the same answer found using the expected value.
Due to the concept of the house edge, casinos know that in the long run, every time a bet is made in roulette, the house averages a profit of $0.0526 for each dollar bet. Yes, gamblers do win at the roulette table and large amounts of money are paid out. But in the long run, the game is a money maker for the casino.
Acknowledgments
This work was made possible by grants from the National Institute of General Medical Sciences—NIGMS (P20GM103446) from the National Institutes of Health (DE-INBRE IDeA program), a National Science Foundation (NSF) EPSCoR grant IIA-1301765 (DE-EPSCoR program) and the Delaware (DE) Economic Development Office (DEDO program). The undergraduates acknowledge tuition scholarship support from Wesley’s NSF S-STEM Cannon Scholar Program (NSF DUE 1355554) and RB acknowledges further support from the NASA DE-Space Grant Consortium (DESGC) program (NASA NNX15AI19H). The DE-INBRE, the DE-EPSCoR and the DESGC grants were obtained through the leadership of the University of Delaware and the authors sincerely appreciate their efforts.
Author contributions
Drs. D’Souza, Wentzien and Nwogbaga served as undergraduate research mentors to Brandenberg, Bautista and Miller, respectively. Professor Olsen has developed and taught the probability and expected value examples in his freshman-level mathematics core courses. The findings and conclusions drawn within the chapter in no way reflect the interpretations and/or views of any other federal or state agency.
Conflicts of interest
The authors declare no conflict of interest.
- 1. D’Souza, M.J., Curran, K.L., Olsen, P.E., Nwogbaga, A.P., Stotts, S. Integrative Approach for a Transformative Freshman-Level STEM Curriculum. Journal College Teaching & Learning, 2016; 13 :47–64.
- 2. D’Souza, M.J., Kashmar, R.J., Hurst, K., Fiedler, F., Gross, C.E., Deol, J.K., Wilson, A. Integrative Wesley College Biological Chemistry Program Includes the Use of Informatics Tools, GIS and SAS Software Applications. Contemporary Issues in Education Research, 2015; 8 :193–214.
- 3. Kevill, D.N., D’Souza, M.J. Sixty Years of the Grunwald-Winstein Equation: Development and Recent Applications. Journal of Chemical Research, 2008; 61–66.
- 4. D’Souza, M. J., Kevill, D.N. Application of the Grunwald-Winstein Equations to Studies of Solvolytic Reactions of Chloroformate and Fluoroformate Esters. Review Chapter in Research Recent Developments in Organic Chemistry, 2013; 13 :1–38, Editor, S.G. Pandalai. Transworld Research Network, Kerala, India, ISBN: 978-81-7895-600-8.
- 5. Kevill, D.N., D’Souza, M.J. Correlation of the Rates of Solvolysis of Benzoyl Fluoride and a Consideration of Leaving-Group Effects. Journal of Organic Chemistry, 2004; 69 :7044–7050.
- 6. Kevill, D.N., D’Souza, M.J. Correlation of the Rates of Solvolysis of Benzoyl Chloride and Derivatives Using Extended Forms of the Grunwald-Winstein Equation. Journal of Physical Organic Chemistry, 2002; 15 :881–888.
- 7. Kim, J.W., Lee, I., Sohn, S.C., Uhm, T.S. Solvolysis of Benzoyl Cyanide, Journal of the Korean Chemical Society, 1983; 27 :95–101.
- 8. Centers for Disease Control and Prevention (2016): 2014 Ebola Outbreak in West Africa. Retrieved from http://www.cdc.gov/vhf/ebola/outbreaks/2014-west-africa/index.html.
- 9. World Health Organization. Global Alert and Response: Ebola Virus Disease (EVD). Geneva, Switzerland: World Health Organization; 2014. Available at http://www.who. int/csr/don/archive/disease/ebola/en.
© 2017 The Author(s). Licensee IntechOpen. This chapter is distributed under the terms of the Creative Commons Attribution 3.0 License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Continue reading from the same book
Published: 26 April 2017
By Aris Spanos
1542 downloads
By Hong Son Hoang and Remy Baraille
1560 downloads
By Agnar Höskuldsson
1413 downloads
IntechOpen Author/Editor? To get your discount, log in .
Discounts available on purchase of multiple copies. View rates
Local taxes (VAT) are calculated in later steps, if applicable.
| : .” .” .” .” .” and the for each type of statistics. ” (a transcript of the video is available ). essay (using examples to support) the thesis that “Descriptive statistics are useful.” Remember that descriptive statistics can be graphs and figures, as well as means and modes. And remember to use examples of descriptive statistics, not reasons to use descriptive statistics. has a and a . sentence that . . . and ends with something (mildly) witty or profound. sentence that . of your paragraphs — your Introduction Paragraph, each of your three Examples Paragraphs, and your Conclusion Paragraph — to make sure each of your five paragraphs has (a Topic Sentence, three Supporting Sentences, and a Conclusion Sentence). (i.e., your readers need to be able to trace the source of any words or any ideas — even if you have summarized those words or ideas — if they are not your own words or ideas). . essay (using examples to support), this time to support the thesis “Inferential statistics are useful.” Remember to use examples of inferential statistics, not reasons to use inferential statistics. has a and a . sentence that . . . sentence that . of your paragraphs — your Introduction Paragraph, each of your three Examples Paragraphs, and your Conclusion Paragraph — to make sure each of your five paragraphs has (a Topic Sentence, three Supporting Sentences, and a Conclusion Sentence). (i.e., your readers need to be able to trace the source of any words or any ideas — even if you have summarized those words or ideas — if they are not your own words or ideas). , who is widely considered the father of U.S. Psychology! and make a new Discussion Board post. : by Darrell Huff. favorite deceptions. For example, you might choose as one of your favorite deceptions the hypothetical real estate agent’s deceptive use of a neighborhood’s “average” income in Chapter 2. favorite deceptions to other people. ). . . and make a new Discussion Board post.: .” .” Seven Sins of Statistical Misinterpretation” to scientific articles you have read. that you found and read in Unit #5 and that you synthesized in Unit #6. .” . _PSY-225_Gernsbacher_StatsCheck_Fillable.pdf. In other words, add your last name to the beginning of the filename. you open the unfilled PDF from your computer. and attach your filled-in PDF.: .” .” .” of the following five topics for which Gallup has conducted a public opinion poll. Then, within each of the three topics you’ve chosen, read of the listed reports. ” ” ” ” ” ” ” ” ” ” ” ” ” ” ” ” ” ” ” ” and make a new post of at least in which you provide the following information for you chose to read (three topics x one report per topic). It will be easiest if you write a separate paragraph for .: and read all the other students’ posts. other students; each of your three responses should be . that you also wrote about. . (besides the two students you responded to in 1. and 2. above).: . If you are in a Chat Group with two other students, that means you will read four essays; if you are in a Chat Group with only one other student, that means you will read two essays. . Note that you will again be answering 12 questions about each member’s essays. text-based Chat. . ” images. More than one Chat Group member can indicate the same image if that’s how they are feeling, and please refer to each image by its number , , that summarizes your Group Chat in . , save the Chat transcript, as described in the (under the topic, “How To Save and Attach a Chat Transcript”), and attach the Chat transcript, in PDF, to a post on the . , that states the name of the assignment (Unit 7: Assignment #6), the full name of your Chat Group, the first and last names of each Chat Group member who participated in the Group Chat, the day (e.g., Sunday) and date of this Group Chat (e.g., June 13), the start and stop time of this Group Chat (e.g., 1pm to 2pm). ” images. More than one Chat Group member can indicate the same image if that’s how they are feeling, and please refer to each image by its number. : The “How Are You Feeling at the of Today’s Group Chat” grid of images differs from the “How Are You Feeling at the of Today’s Group Chat” grid of images.Congratulations, you have finished Unit 7! Onward to ! |

An introduction to inferential statistics: A review and practical guide
- February 2011
- Radiography 17(1)
- This person is not on ResearchGate, or hasn't claimed this research yet.

- North Cumbria Integrated Care NHS FT
Discover the world's research
- 25+ million members
- 160+ million publication pages
- 2.3+ billion citations
No full-text available
To read the full-text of this research, you can request a copy directly from the authors.

- PA Shenjere
- SJ Ferreira-Schenk

- Rural Rem Health

- Aggrey Dhabangi

- Umesh Acharya

- Environ Dev Sustain

- RADIAT PROT DOSIM
- Shauna Daly
- Cliona Skelly

- Rachel Toomey

- MON NOT R ASTRON SOC

- Trienko Grobler
- Stefan J. Wijnholds

- Anugrah Pratap

- Rainier Thomas A. Antonio
- Lorraine Anne A. Bergado
- Joliber M. Caminong

- Himanshu Soni
- Ronald Laban

- Leni Anggraeni

- Michail Prodromou

- Ioannis Politis

- Zamhuri Rachman

- Sheikh Md. Imran

- farida islamiah

- Khalijah Hussain
- Wan Ahmad Munsif Wan Pa
- Hayley Langfield
- Muhammad Fath Kathin

- Radiography

- V.J. Hughes
- Promise Magoma

- J Martin Bland
- ADV PHYSIOL EDUC

- Alison M MacLeod

- Pauline A Waight
- G. D. Murray
- L. V. Glickman
- D. Rowntree
- Clin Chiropract
- Jenni Bolton

- Martin Bland
- J AM STAT ASSOC
- Jacob Cohen

- Aust Crit Care

- Elizabeth K. Dawson-Saunders
- J. Roland Folse
- Judy M Simpson
- J.N.S. Matthews
- A Gouveia-Oliveira
- Elizabeth Miller

- Manag Care Q
- Jeroan J. Allison
- J W Calhoun
- Terry C Wall

- NURS EDUC TODAY
- David Justham

- CLIN CHIM ACTA
- A Ralph Henderson
- Petropoulos C M I Farrington
- A Edmondson
- Recruit researchers
- Join for free
- Login Email Tip: Most researchers use their institutional email address as their ResearchGate login Password Forgot password? Keep me logged in Log in or Continue with Google Welcome back! Please log in. Email · Hint Tip: Most researchers use their institutional email address as their ResearchGate login Password Forgot password? Keep me logged in Log in or Continue with Google No account? Sign up
- How it works

Inferential Statistics – Guide With Examples
Published by Jamie Walker at August 25th, 2021 , Revised On December 12, 2022
Statistics students must have heard a lot of times that inferential statistics is the heart of statistics. Well, that is true and reasonable. While descriptive statistics are easy to comprehend, inferential statistics are pretty complex and often have different interpretations.
If you are also confused about how descriptive and inferential statistics are different, this blog is for you. Everything from the definition of inferential statistics to its examples and uses is all mentioned here.
Having that said, let’s start with where statistics initially came from.

Inferential Statistics: An Introduction
To know the origin and definition of inferential statistics, you must know what statistics is and how it came to be.
So, statistics is the branch of math that deals with collecting, assessing, and interpreting data. It includes how this data is presented in the form of numbers and digits. In other words, statistics is the study of quantitative or numerical data.
Statistics is broadly divided into two departments, namely Applied Statistics and Theoretical Statistics. Applied Statistics are further categorized into two sub-groups: Descriptive Statistics and Inferential Statistics.
There are two main areas of Inferential Statistics:
- Estimating Parameters: It means taking a statistic from a sample and utilizing it to describe something about a population .
- Hypothesis Testing : it is when you use this sample data to answer various research questions .
Now let’s delve down deeper and see how descriptive and inferential statistics are different from each other.
Inferential Statistics vs. Descriptive Statistics
Descriptive statistics allow you to explain a data set, while inferential statistics allow you to make inferences or interpretations based on a particular data set.
Here are a few differences between inferential and descriptive statistics:
Firstly , descriptive statistics can be used to describe a particular situation, while inferential statistics are used to dig deeper into the chances of occurrence of a condition.
Secondly , descriptive statistics give information about raw data and how it is organized in a particular manner. The other one, on the contrary, compares data and helps you make predictions and hypotheses with it.
Lastly , descriptive statistics are shown with charts, graphs, and tables, while inferential statistics are achieved via probability. Descriptive statistics have a diagrammatic or tabular representation of the final outcomes, and inferential statistics show results in the probability form.
Are we clear about the differences between these two? Let move on to the next topic then.
Sampling Error and Inferential Statistics
Can you recall the sample and population? How about statistics and parameters? Great, if you can.
Here is a quick recap for those who cannot remember these terms.
Sample: A sample is a small group taken from the population to observe and draw conclusions. Population: It is the entire group under study. Statistic: A statistic is a number that describes a sample. For instance, the sample mean. Parameter: It is a number that describes the whole population. For instance, a population mean.
Why should you use a Plagiarism Detector for your Paper?
It ensures:
- Original work
- Structure and Clarity
- Zero Spelling Errors
- No Punctuation Faults

The fact that the size of the sample is much smaller than that of a population, there is a great chance that some of the population is not captured by the sample data. Hence, there is always room for error, which we call sampling error in statistics. It is the difference between the true population values and the captured population values. In other words, it is the difference between parameters and statistics.
A sampling error can occur any time you examine a sample, regardless of the sampling technique, i.e., random or systematic sampling. This is why there is some uncertainty in inferential statistics, no matter what. However, this can be reduced using probability sampling methods.
You can make two kinds of estimates about the population:
Point Estimate -it is a single value estimate of a population parameter.
Interval Estimate -it gives you a wide range of values where the parameter is predicted to lie.
Have you heard of a confidence interval? That is the most used type of interval estimate.
Details are below:
Confidence Intervals
Confidence intervals tend to use the variability around a sample statistic to deduce an interval estimate for a parameter. They are used for finding parameters because they assess the sampling errors. For instance, if a point estimate reflects a precise value for the population parameter, confidence intervals give you an estimate of the uncertainty of the point estimate.
All these confidence intervals are associated with confidence levels that tell you about the probability of the interval containing the population parameter estimate on repeating the study.
An 85 percent confidence interval means that if you repeat the research with a new sample precisely the same way 100 times, you can predict the estimate to lie within the range of values 85 times.
You might expect the estimate to lie within the interval a certain percentage of the time, but you cannot be 100% confident that the actual population parameter will. It is simply because you cannot predict the true value of the parameter without gathering data from the whole population.
However, with suitable sample size and random sampling, you can expect the confidence interval to contain the population parameter a certain percentage of the time.
Hypothesis Testing and Inferential Statistics
Hypothesis testing is a practice of inferential statistics that aims to deduce conclusions based on a sample about the whole population. It allows us to compare different populations in order to come to a certain supposition.
These hypotheses are then tested using statistical tests , which also predict sampling errors to make accurate inferences. Statistical tests are either parametric or non-parametric. Parametric tests are thought to be more powerful from a statistics point of view, as they can detect an existing effect more likely.
Some of the assumptions parametric tests make are:
- Sample of a population follows a normal distribution of scores
- The sample size is big enough to represent the whole the population
- A measure of the spread of all groups compared are same
Non-parametric tests are not effective when the data at hand violates any of the assumptions mentioned above. The fact that non-parametric tests do not assume anything about the population distribution they are called “distribution-free tests.”
Forms of Statistical Tests
The statistical tests can be of three types or come in three versions:
Comparison Tests
Correlation Tests
Regression Tests
As the name suggests, comparison tests evaluate and see if there are differences in means and medians . They also assess the difference in rankings of scores of two or multiple groups.
The correlation tests allow us to determine the extent to which two or more variables are associated with each other.
Lastly, the regression tests tell whether the changes in predictor variables are causing changes in the outcome variable or not. Depending on the number and type of variables you have as outcomes and predictors, you can decide which regression test suits you the best.
FAQs About Inferential Statistics
1. what are the two main branches of statistics.
Statistics is broadly divided into two departments, namely Applied Statistics, and Theoretical Statistics. Applied Statistics are further categorized into two sub-groups: Descriptive Statistics and Inferential Statistics.
2. What are inferential statistics?
They help us compare data and make predictions with it. Inferential statistics allow you to assess a test hypothesis and see whether data is generating the whole population or not.
3. What are statistics and parameters?
Statistic: A statistic is a number that defines a sample. For instance, the sample mean .
Parameter: It is a number that describes the whole population. For instance, a population mean.
4. Define sampling error.
It is the difference between the true population values and the captured population values.
5. What are the three forms of statistical tests?
The correlation tests allow us to find out the extent to which two or more variables are associated with each other.
The regression tests tell whether the changes in predictor variables are causing changes in the outcome variable or not.
6. What is hypothesis testing?
Hypothesis testing is a kind of inferential statistics that aims to deduce conclusions based on samples about the whole population. It allows us to compare different populations in order to come to a certain supposition.
You May Also Like
This introductory article aims to define, elaborate and exemplify transferability in qualitative research.
There may be two kinds of errors that can occur when testing your hypothesis. These errors are known as the Type 1 error and the Type 2 error.
Ordinal data, as the name itself suggests, has its variables in a specific hierarchy or order. It is categorical data with a set scale or order to it.
USEFUL LINKS
LEARNING RESOURCES

COMPANY DETAILS

- How It Works
Have a thesis expert improve your writing
Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.
- Knowledge Base
- Inferential Statistics | An Easy Introduction & Examples
Inferential Statistics | An Easy Introduction & Examples
Published on 18 January 2023 by Pritha Bhandari .
While descriptive statistics summarise the characteristics of a data set, inferential statistics help you come to conclusions and make predictions based on your data.
When you have collected data from a sample , you can use inferential statistics to understand the larger population from which the sample is taken.
Inferential statistics have two main uses:
- making estimates about populations (for example, the mean SAT score of all 11th graders in the US).
- testing hypotheses to draw conclusions about populations (for example, the relationship between SAT scores and family income).
Table of contents
Descriptive versus inferential statistics, estimating population parameters from sample statistics, hypothesis testing, frequently asked questions.
Descriptive statistics allow you to describe a data set, while inferential statistics allow you to make inferences based on a data set.
Descriptive statistics
Using descriptive statistics, you can report characteristics of your data:
- The distribution concerns the frequency of each value.
- The central tendency concerns the averages of the values.
- The variability concerns how spread out the values are.
In descriptive statistics, there is no uncertainty – the statistics precisely describe the data that you collected. If you collect data from an entire population, you can directly compare these descriptive statistics to those from other populations.
Inferential statistics
Most of the time, you can only acquire data from samples, because it is too difficult or expensive to collect data from the whole population that you’re interested in.
While descriptive statistics can only summarise a sample’s characteristics, inferential statistics use your sample to make reasonable guesses about the larger population.
With inferential statistics, it’s important to use random and unbiased sampling methods . If your sample isn’t representative of your population, then you can’t make valid statistical inferences or generalise .
Sampling error in inferential statistics
Since the size of a sample is always smaller than the size of the population, some of the population isn’t captured by sample data. This creates sampling error , which is the difference between the true population values (called parameters) and the measured sample values (called statistics).
Sampling error arises any time you use a sample, even if your sample is random and unbiased. For this reason, there is always some uncertainty in inferential statistics. However, using probability sampling methods reduces this uncertainty.
The characteristics of samples and populations are described by numbers called statistics and parameters :
- A statistic is a measure that describes the sample (e.g., sample mean ).
- A parameter is a measure that describes the whole population (e.g., population mean).
Sampling error is the difference between a parameter and a corresponding statistic. Since in most cases you don’t know the real population parameter, you can use inferential statistics to estimate these parameters in a way that takes sampling error into account.
There are two important types of estimates you can make about the population: point estimates and interval estimates .
- A point estimate is a single value estimate of a parameter. For instance, a sample mean is a point estimate of a population mean.
- An interval estimate gives you a range of values where the parameter is expected to lie. A confidence interval is the most common type of interval estimate.
Both types of estimates are important for gathering a clear idea of where a parameter is likely to lie.
Confidence intervals
A confidence interval uses the variability around a statistic to come up with an interval estimate for a parameter. Confidence intervals are useful for estimating parameters because they take sampling error into account.
While a point estimate gives you a precise value for the parameter you are interested in, a confidence interval tells you the uncertainty of the point estimate. They are best used in combination with each other.
Each confidence interval is associated with a confidence level. A confidence level tells you the probability (in percentage) of the interval containing the parameter estimate if you repeat the study again.
A 95% confidence interval means that if you repeat your study with a new sample in exactly the same way 100 times, you can expect your estimate to lie within the specified range of values 95 times.
Although you can say that your estimate will lie within the interval a certain percentage of the time, you cannot say for sure that the actual population parameter will. That’s because you can’t know the true value of the population parameter without collecting data from the full population.
However, with random sampling and a suitable sample size, you can reasonably expect your confidence interval to contain the parameter a certain percentage of the time.
Your point estimate of the population mean paid vacation days is the sample mean of 19 paid vacation days.
Hypothesis testing is a formal process of statistical analysis using inferential statistics. The goal of hypothesis testing is to compare populations or assess relationships between variables using samples.
Hypotheses , or predictions, are tested using statistical tests . Statistical tests also estimate sampling errors so that valid inferences can be made.
Statistical tests can be parametric or non-parametric. Parametric tests are considered more statistically powerful because they are more likely to detect an effect if one exists.
Parametric tests make assumptions that include the following:
- the population that the sample comes from follows a normal distribution of scores
- the sample size is large enough to represent the population
- the variances , a measure of variability , of each group being compared are similar
When your data violates any of these assumptions, non-parametric tests are more suitable. Non-parametric tests are called ‘distribution-free tests’ because they don’t assume anything about the distribution of the population data.
Statistical tests come in three forms: tests of comparison, correlation or regression.
Comparison tests
Comparison tests assess whether there are differences in means, medians or rankings of scores of two or more groups.
To decide which test suits your aim, consider whether your data meets the conditions necessary for parametric tests, the number of samples, and the levels of measurement of your variables.
Means can only be found for interval or ratio data , while medians and rankings are more appropriate measures for ordinal data .
| test | Yes | Means | 2 samples |
|---|---|---|---|
| Yes | Means | 3+ samples | |
| Mood’s median | No | Medians | 2+ samples |
| Wilcoxon signed-rank | No | Distributions | 2 samples |
| Wilcoxon rank-sum (Mann-Whitney ) | No | Sums of rankings | 2 samples |
| Kruskal-Wallis | No | Mean rankings | 3+ samples |
Correlation tests
Correlation tests determine the extent to which two variables are associated.
Although Pearson’s r is the most statistically powerful test, Spearman’s r is appropriate for interval and ratio variables when the data doesn’t follow a normal distribution.
The chi square test of independence is the only test that can be used with nominal variables.
| Pearson’s | Yes | Interval/ratio variables |
|---|---|---|
| Spearman’s | No | Ordinal/interval/ratio variables |
| Chi square test of independence | No | Nominal/ordinal variables |
Regression tests
Regression tests demonstrate whether changes in predictor variables cause changes in an outcome variable. You can decide which regression test to use based on the number and types of variables you have as predictors and outcomes.
Most of the commonly used regression tests are parametric. If your data is not normally distributed, you can perform data transformations.
Data transformations help you make your data normally distributed using mathematical operations, like taking the square root of each value.
| 1 interval/ratio variable | 1 interval/ratio variable | |
| 2+ interval/ratio variable(s) | 1 interval/ratio variable | |
| Logistic regression | 1+ any variable(s) | 1 binary variable |
| Nominal regression | 1+ any variable(s) | 1 nominal variable |
| Ordinal regression | 1+ any variable(s) | 1 ordinal variable |
Descriptive statistics summarise the characteristics of a data set. Inferential statistics allow you to test a hypothesis or assess whether your data is generalisable to the broader population.
A statistic refers to measures about the sample , while a parameter refers to measures about the population .
A sampling error is the difference between a population parameter and a sample statistic .
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.
Bhandari, P. (2023, January 18). Inferential Statistics | An Easy Introduction & Examples. Scribbr. Retrieved 5 August 2024, from https://www.scribbr.co.uk/stats/inferential-statistics-meaning/
Is this article helpful?

Pritha Bhandari
Other students also liked, descriptive statistics | definitions, types, examples, understanding confidence intervals | easy examples & formulas, how to calculate variance | calculator, analysis & examples.
Inferential statistics
- First Online: 01 September 2023
Cite this chapter

- Matthias Plaue 2
1345 Accesses
Inferential statistics is based on the assumption that data are realizations of random variables.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Compact, lightweight edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Unable to display preview. Download preview PDF.
Author information
Authors and affiliations.
MAPEGY GmbH, Berlin, Germany
Matthias Plaue
You can also search for this author in PubMed Google Scholar
Rights and permissions
Reprints and permissions
Copyright information
© 2023 Springer-Verlag GmbH Germany, part of Springer Nature
About this chapter
Plaue, M. (2023). Inferential statistics. In: Data Science. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-67882-4_4
Download citation
DOI : https://doi.org/10.1007/978-3-662-67882-4_4
Published : 01 September 2023
Publisher Name : Springer, Berlin, Heidelberg
Print ISBN : 978-3-662-67881-7
Online ISBN : 978-3-662-67882-4
eBook Packages : Computer Science Computer Science (R0)
Share this chapter
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Choosing the Right Statistical Test | Types & Examples
Choosing the Right Statistical Test | Types & Examples
Published on January 28, 2020 by Rebecca Bevans . Revised on June 22, 2023.
Statistical tests are used in hypothesis testing . They can be used to:
- determine whether a predictor variable has a statistically significant relationship with an outcome variable.
- estimate the difference between two or more groups.
Statistical tests assume a null hypothesis of no relationship or no difference between groups. Then they determine whether the observed data fall outside of the range of values predicted by the null hypothesis.
If you already know what types of variables you’re dealing with, you can use the flowchart to choose the right statistical test for your data.
Statistical tests flowchart
Table of contents
What does a statistical test do, when to perform a statistical test, choosing a parametric test: regression, comparison, or correlation, choosing a nonparametric test, flowchart: choosing a statistical test, other interesting articles, frequently asked questions about statistical tests.
Statistical tests work by calculating a test statistic – a number that describes how much the relationship between variables in your test differs from the null hypothesis of no relationship.
It then calculates a p value (probability value). The p -value estimates how likely it is that you would see the difference described by the test statistic if the null hypothesis of no relationship were true.
If the value of the test statistic is more extreme than the statistic calculated from the null hypothesis, then you can infer a statistically significant relationship between the predictor and outcome variables.
If the value of the test statistic is less extreme than the one calculated from the null hypothesis, then you can infer no statistically significant relationship between the predictor and outcome variables.
Prevent plagiarism. Run a free check.
You can perform statistical tests on data that have been collected in a statistically valid manner – either through an experiment , or through observations made using probability sampling methods .
For a statistical test to be valid , your sample size needs to be large enough to approximate the true distribution of the population being studied.
To determine which statistical test to use, you need to know:
- whether your data meets certain assumptions.
- the types of variables that you’re dealing with.
Statistical assumptions
Statistical tests make some common assumptions about the data they are testing:
- Independence of observations (a.k.a. no autocorrelation): The observations/variables you include in your test are not related (for example, multiple measurements of a single test subject are not independent, while measurements of multiple different test subjects are independent).
- Homogeneity of variance : the variance within each group being compared is similar among all groups. If one group has much more variation than others, it will limit the test’s effectiveness.
- Normality of data : the data follows a normal distribution (a.k.a. a bell curve). This assumption applies only to quantitative data .
If your data do not meet the assumptions of normality or homogeneity of variance, you may be able to perform a nonparametric statistical test , which allows you to make comparisons without any assumptions about the data distribution.
If your data do not meet the assumption of independence of observations, you may be able to use a test that accounts for structure in your data (repeated-measures tests or tests that include blocking variables).
Types of variables
The types of variables you have usually determine what type of statistical test you can use.
Quantitative variables represent amounts of things (e.g. the number of trees in a forest). Types of quantitative variables include:
- Continuous (aka ratio variables): represent measures and can usually be divided into units smaller than one (e.g. 0.75 grams).
- Discrete (aka integer variables): represent counts and usually can’t be divided into units smaller than one (e.g. 1 tree).
Categorical variables represent groupings of things (e.g. the different tree species in a forest). Types of categorical variables include:
- Ordinal : represent data with an order (e.g. rankings).
- Nominal : represent group names (e.g. brands or species names).
- Binary : represent data with a yes/no or 1/0 outcome (e.g. win or lose).
Choose the test that fits the types of predictor and outcome variables you have collected (if you are doing an experiment , these are the independent and dependent variables ). Consult the tables below to see which test best matches your variables.
Parametric tests usually have stricter requirements than nonparametric tests, and are able to make stronger inferences from the data. They can only be conducted with data that adheres to the common assumptions of statistical tests.
The most common types of parametric test include regression tests, comparison tests, and correlation tests.
Regression tests
Regression tests look for cause-and-effect relationships . They can be used to estimate the effect of one or more continuous variables on another variable.
| Predictor variable | Outcome variable | Research question example | |
|---|---|---|---|
| What is the effect of income on longevity? | |||
| What is the effect of income and minutes of exercise per day on longevity? | |||
| Logistic regression | What is the effect of drug dosage on the survival of a test subject? |
Comparison tests
Comparison tests look for differences among group means . They can be used to test the effect of a categorical variable on the mean value of some other characteristic.
T-tests are used when comparing the means of precisely two groups (e.g., the average heights of men and women). ANOVA and MANOVA tests are used when comparing the means of more than two groups (e.g., the average heights of children, teenagers, and adults).
| Predictor variable | Outcome variable | Research question example | |
|---|---|---|---|
| Paired t-test | What is the effect of two different test prep programs on the average exam scores for students from the same class? | ||
| Independent t-test | What is the difference in average exam scores for students from two different schools? | ||
| ANOVA | What is the difference in average pain levels among post-surgical patients given three different painkillers? | ||
| MANOVA | What is the effect of flower species on petal length, petal width, and stem length? |
Correlation tests
Correlation tests check whether variables are related without hypothesizing a cause-and-effect relationship.
These can be used to test whether two variables you want to use in (for example) a multiple regression test are autocorrelated.
| Variables | Research question example | |
|---|---|---|
| Pearson’s | How are latitude and temperature related? |
Non-parametric tests don’t make as many assumptions about the data, and are useful when one or more of the common statistical assumptions are violated. However, the inferences they make aren’t as strong as with parametric tests.
| Predictor variable | Outcome variable | Use in place of… | |
|---|---|---|---|
| Spearman’s | |||
| Pearson’s | |||
| Sign test | One-sample -test | ||
| Kruskal–Wallis | ANOVA | ||
| ANOSIM | MANOVA | ||
| Wilcoxon Rank-Sum test | Independent t-test | ||
| Wilcoxon Signed-rank test | Paired t-test | ||
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

This flowchart helps you choose among parametric tests. For nonparametric alternatives, check the table above.
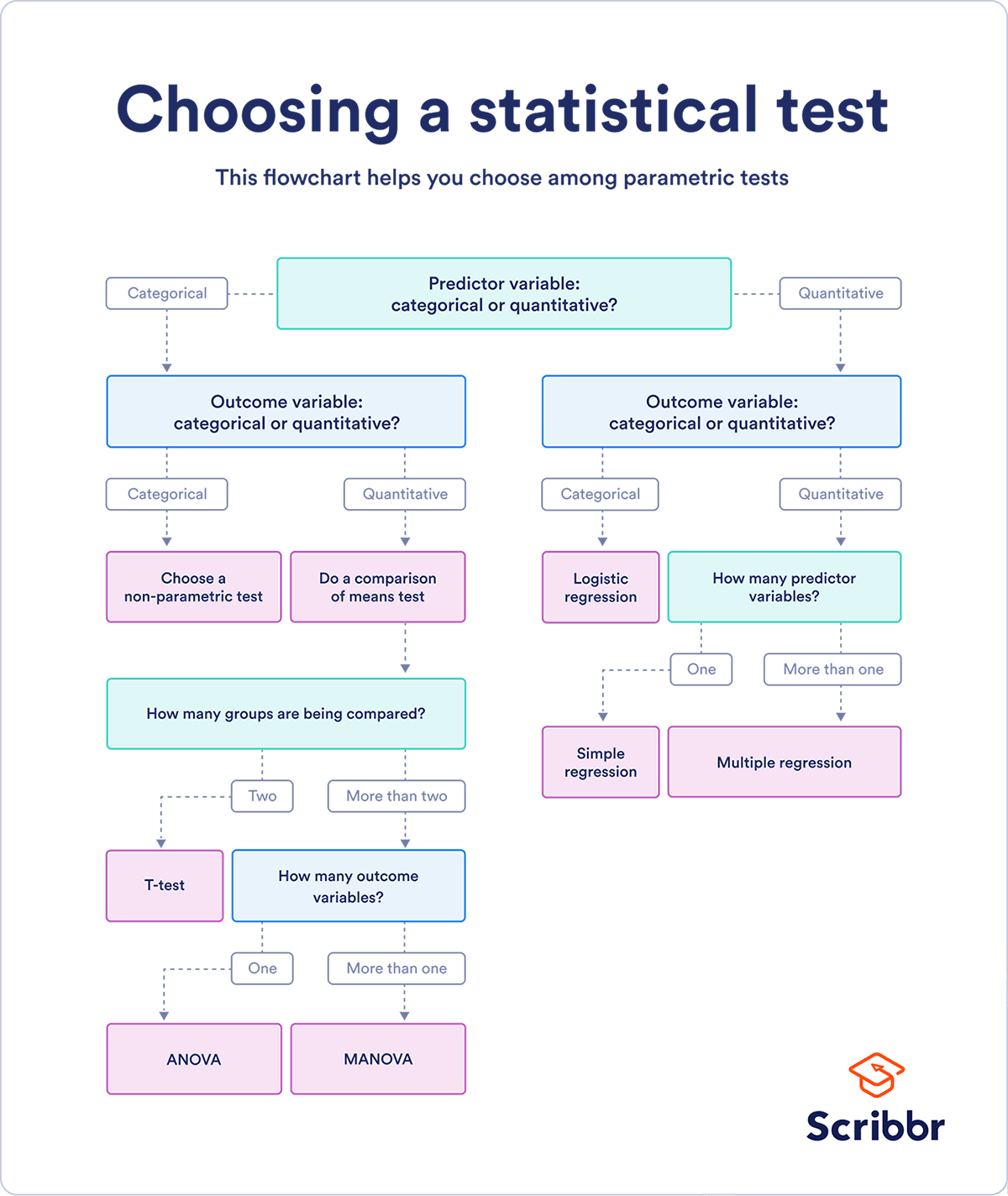
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
- Null hypothesis
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Statistical tests commonly assume that:
- the data are normally distributed
- the groups that are being compared have similar variance
- the data are independent
If your data does not meet these assumptions you might still be able to use a nonparametric statistical test , which have fewer requirements but also make weaker inferences.
A test statistic is a number calculated by a statistical test . It describes how far your observed data is from the null hypothesis of no relationship between variables or no difference among sample groups.
The test statistic tells you how different two or more groups are from the overall population mean , or how different a linear slope is from the slope predicted by a null hypothesis . Different test statistics are used in different statistical tests.
Statistical significance is a term used by researchers to state that it is unlikely their observations could have occurred under the null hypothesis of a statistical test . Significance is usually denoted by a p -value , or probability value.
Statistical significance is arbitrary – it depends on the threshold, or alpha value, chosen by the researcher. The most common threshold is p < 0.05, which means that the data is likely to occur less than 5% of the time under the null hypothesis .
When the p -value falls below the chosen alpha value, then we say the result of the test is statistically significant.
Quantitative variables are any variables where the data represent amounts (e.g. height, weight, or age).
Categorical variables are any variables where the data represent groups. This includes rankings (e.g. finishing places in a race), classifications (e.g. brands of cereal), and binary outcomes (e.g. coin flips).
You need to know what type of variables you are working with to choose the right statistical test for your data and interpret your results .
Discrete and continuous variables are two types of quantitative variables :
- Discrete variables represent counts (e.g. the number of objects in a collection).
- Continuous variables represent measurable amounts (e.g. water volume or weight).
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). Choosing the Right Statistical Test | Types & Examples. Scribbr. Retrieved August 5, 2024, from https://www.scribbr.com/statistics/statistical-tests/
Is this article helpful?
Rebecca Bevans
Other students also liked, hypothesis testing | a step-by-step guide with easy examples, test statistics | definition, interpretation, and examples, normal distribution | examples, formulas, & uses, what is your plagiarism score.
Popular searches
- How to Get Participants For Your Study
- How to Do Segmentation?
- Conjoint Preference Share Simulator
- MaxDiff Analysis
- Likert Scales
- Reliability & Validity
Request consultation
Do you need support in running a pricing or product study? We can help you with agile consumer research and conjoint analysis.
Looking for an online survey platform?
Conjointly offers a great survey tool with multiple question types, randomisation blocks, and multilingual support. The Basic tier is always free.
Research Methods Knowledge Base
- Navigating the Knowledge Base
- Foundations
- Measurement
- Research Design
- Conclusion Validity
- Data Preparation
- Descriptive Statistics
- Dummy Variables
- General Linear Model
- Posttest-Only Analysis
- Factorial Design Analysis
- Randomized Block Analysis
- Analysis of Covariance
- Nonequivalent Groups Analysis
- Regression-Discontinuity Analysis
- Regression Point Displacement
- Table of Contents
Fully-functional online survey tool with various question types, logic, randomisation, and reporting for unlimited number of surveys.
Completely free for academics and students .
Inferential Statistics
With inferential statistics, you are trying to reach conclusions that extend beyond the immediate data alone. For instance, we use inferential statistics to try to infer from the sample data what the population might think. Or, we use inferential statistics to make judgments of the probability that an observed difference between groups is a dependable one or one that might have happened by chance in this study. Thus, we use inferential statistics to make inferences from our data to more general conditions; we use descriptive statistics simply to describe what’s going on in our data.
Here, I concentrate on inferential statistics that are useful in experimental and quasi-experimental research design or in program outcome evaluation. Perhaps one of the simplest inferential test is used when you want to compare the average performance of two groups on a single measure to see if there is a difference. You might want to know whether eighth-grade boys and girls differ in math test scores or whether a program group differs on the outcome measure from a control group. Whenever you wish to compare the average performance between two groups you should consider the t-test for differences between groups .
Most of the major inferential statistics come from a general family of statistical models known as the General Linear Model . This includes the t-test, Analysis of Variance (ANOVA), Analysis of Covariance (ANCOVA), regression analysis, and many of the multivariate methods like factor analysis, multidimensional scaling, cluster analysis, discriminant function analysis, and so on. Given the importance of the General Linear Model, it’s a good idea for any serious social researcher to become familiar with its workings. The discussion of the General Linear Model here is very elementary and only considers the simplest straight-line model. However, it will get you familiar with the idea of the linear model and help prepare you for the more complex analyses described below.
One of the keys to understanding how groups are compared is embodied in the notion of the “dummy” variable. The name doesn’t suggest that we are using variables that aren’t very smart or, even worse, that the analyst who uses them is a “dummy”! Perhaps these variables would be better described as “proxy” variables. Essentially a dummy variable is one that uses discrete numbers, usually 0 and 1, to represent different groups in your study. Dummy variables are a simple idea that enable some pretty complicated things to happen. For instance, by including a simple dummy variable in an model, I can model two separate lines (one for each treatment group) with a single equation. To see how this works, check out the discussion on dummy variables .
One of the most important analyses in program outcome evaluations involves comparing the program and non-program group on the outcome variable or variables. How we do this depends on the research design we use. research designs are divided into two major types of designs : experimental and quasi-experimental . Because the analyses differ for each, they are presented separately.
Experimental Analysis
The simple two-group posttest-only randomized experiment is usually analyzed with the simple t-test or one-way ANOVA . The factorial experimental designs are usually analyzed with the Analysis of Variance (ANOVA) Model . Randomized Block Designs use a special form of ANOVA blocking model that uses dummy-coded variables to represent the blocks. The Analysis of Covariance Experimental Design uses, not surprisingly, the Analysis of Covariance statistical model .
Quasi-Experimental Analysis
The quasi-experimental designs differ from the experimental ones in that they don’t use random assignment to assign units (e.g. people) to program groups. The lack of random assignment in these designs tends to complicate their analysis considerably. For example, to analyze the Nonequivalent Groups Design (NEGD) we have to adjust the pretest scores for measurement error in what is often called a Reliability-Corrected Analysis of Covariance model . In the Regression-Discontinuity Design , we need to be especially concerned about curvilinearity and model misspecification. Consequently, we tend to use a conservative analysis approach that is based on polynomial regression that starts by overfitting the likely true function and then reducing the model based on the results. The Regression Point Displacement Design has only a single treated unit. Nevertheless, the analysis of the RPD design is based directly on the traditional ANCOVA model.
When you’ve investigated these various analytic models, you’ll see that they all come from the same family – the General Linear Model . An understanding of that model will go a long way to introducing you to the intricacies of data analysis in applied and social research contexts.
Cookie Consent
Conjointly uses essential cookies to make our site work. We also use additional cookies in order to understand the usage of the site, gather audience analytics, and for remarketing purposes.
For more information on Conjointly's use of cookies, please read our Cookie Policy .
Which one are you?
I am new to conjointly, i am already using conjointly.

IMAGES
VIDEO
COMMENTS
Example: Inferential statistics. You randomly select a sample of 11th graders in your state and collect data on their SAT scores and other characteristics. You can use inferential statistics to make estimates and test hypotheses about the whole population of 11th graders in the state based on your sample data.
Note that different fields have their own way of writing with statistics—please refer to your field's style guide for specific guidelines. When using a complicated inferential procedure that your readers would be unfamiliar with, explain it. It may be necessary to go over it in detail. You may want to cite who used it first, and why they used ...
The goal in classic inferential statistics is to prove the null hypothesis wrong. The logic says that if the two groups aren't the same, then they must be different. A low p-value indicates a low probability that the null hypothesis is correct (thus, providing evidence for the alternative hypothesis).
of inferential statistics as real life conclusions. One of the main goals of using simulations in a classroom is to create a deeper conceptual understanding of inferential statistics. Students need to be able to do more than just calculate a p-value and then recall the rules for whether or not they should reject their null hypothesis.
Three Modes of Statistical Inference. Descriptive Inference: summarizing and exploring data. Inferring "ideal points" from rollcall votes Inferring "topics" from texts and speeches Inferring "social networks" from surveys. Predictive Inference: forecasting out-of-sample data points. Inferring future state failures from past failures ...
Purpose: Descriptive statistics are used to summarize a dataset while the purpose of inferential statistics is to make predictions about a larger population based on a dataset. Scope: Descriptive statistics are limited to only the available data while inferential statistics is designed to extend from the provided sample to the larger population ...
Sure, inferential statistics are used when making predictions or inferences about a population from a sample of data. Here are a few real-time examples: Medical Research: Suppose a pharmaceutical company is developing a new drug and they're currently in the testing phase. They gather a sample of 1,000 volunteers to participate in a clinical ...
The results chapter (also referred to as the findings or analysis chapter) is one of the most important chapters of your dissertation or thesis because it shows the reader what you've found in terms of the quantitative data you've collected. It presents the data using a clear text narrative, supported by tables, graphs and charts.
In inferential statistics, this probability is called the value, 5 per cent is called the significance level (), and the desired relationship between the -value and is denoted as: . The significance level is the maximum level of risk that we are willing to accept as the price of our inference from the sample to the population.
Inferential stats allow you to assess whether patterns in your sample are likely to be present in your population. Some common inferential statistical tests include t-tests, ANOVA, chi-square, correlation and regression. Inferential statistics alone do not prove causation. To identify and measure causal relationships, you need a very specific ...
Undergraduate data science research projects form an integral component of the Wesley College science and mathematics curriculum. In this chapter, we provide examples for hypothesis testing, where statistical methods or strategies are coupled with methodologies using interpolating polynomials, probability and the expected value concept in statistics. These are areas where real-world critical ...
Write another five-paragraph Examples-Style essay (using examples to support), this time to support the thesis "Inferential statistics are useful." Remember to use examples of inferential statistics, not reasons to use inferential statistics. First, check your essay to make sure your Introduction Paragraph has a hook and a Thesis Statement.
Such statistics are known as Inferential statistics (Marshall and Jonker 2011). Therefore, the current study uses inferential statistics to conclude about all glaciers present in Sikkim from a set ...
Unit 7: How to Evaluate Descriptive and Inferential Statistics. ... Write one five-paragraph Examples-Style essay (using examples to support) the thesis that "Descriptive statistics are useful." Remember that descriptive statistics can be graphs and figures, as well as means and modes. And remember to use examples of descriptive statistics ...
Applied Statistics are further categorized into two sub-groups: Descriptive Statistics and Inferential Statistics. There are two main areas of Inferential Statistics: Estimating Parameters: It means taking a statistic from a sample and utilizing it to describe something about a population. Hypothesis Testing: it is when you use this sample data ...
Step 4: Test hypotheses or make estimates with inferential statistics. A number that describes a sample is called a statistic, while a number describing a population is called a parameter. Using inferential statistics, you can make conclusions about population parameters based on sample statistics.
and figures. In Section 4, some notes about the rules of conduct when writing a master's thesis are provided. 2 The Structure of a Master's Thesis A master's thesis is an independent scientific work and is meant to prepare students for future professional or academic work. Largely, the thesis is expected to be similar to papers published in
Example: Inferential statistics. You randomly select a sample of 11th graders in your state and collect data on their SAT scores and other characteristics. You can use inferential statistics to make estimates and test hypotheses about the whole population of 11th graders in the state based on your sample data.
M. Baz, PhD Thesis, University of York 2014 Abstract This thesis explores the issues and techniques associated with employing the principles of inferential statistics to design effective Medium Access Control (MAC), routing and duty cycle management strategies for multihop Wireless Sensor Networks (WSNs).
Inferential statistics is based on the assumption that data are realizations of random variables. Download to read the full chapter text. Chapter PDF. Author information. Authors and Affiliations. MAPEGY GmbH, Berlin, Germany. Matthias Plaue. Authors. Matthias Plaue. View author publications.
ANOVA and MANOVA tests are used when comparing the means of more than two groups (e.g., the average heights of children, teenagers, and adults). Predictor variable. Outcome variable. Research question example. Paired t-test. Categorical. 1 predictor. Quantitative. groups come from the same population.
Inferential Statistics. With inferential statistics, you are trying to reach conclusions that extend beyond the immediate data alone. For instance, we use inferential statistics to try to infer from the sample data what the population might think. Or, we use inferential statistics to make judgments of the probability that an observed difference ...
statistics unit described in this study, for his advice. I wish to thank my parents, Kenneth and Phyllis Duck. They did all they could so that their daughters could have the education that they could never have. My fa-ther died during the time this thesis was written; he would have been thrilled to know that it has been finished.